Descomposición en valores singulares y análisis de factores en ciencias humanas y sociales
Singular Value Decomposition and factor analysis in Social Science and Humanities
Sergio A. Pernice
Universidad del CEMA (Argentina)
https://orcid.org/0009-0003-2860-9934
RESUMEN
Los objetos de estudio de las ciencias humanas y sociales son intrínsecamente complejos. Porque es filosóficamente atractiva, y además porque ayuda en la práctica a manejar dicha complejidad, una de las ideas fuerza más influyente a lo largo de la historia y presente de dichas disciplinas, es la noción de que la gran cantidad de manifestaciones empíricas que caracterizan sus objetos de estudio son expresiones de unos pocos factores que influyen sobre todas las demás variables. La correspondiente metodología estadística para implementar esas ideas tiene diferente nombre y difiere en detalles en distintas disciplinas, pero un nombre que puede ser reconocido en muchas de ellas es el “análisis de factores”. El primer objetivo del presente trabajo es presentar un método clásico de álgebra lineal, conocido como la “Descomposición en valores singulares” (SVD), de manera intuitiva y a la vez rigurosa a la comunidad de ciencias humanas y sociales. SVD sistematiza y generaliza la descomposición en factores de cualquier matriz de datos. Además, el método es de enorme importancia en la era de big data y machine learning, que influye en todas las áreas de estudio. El segundo objetivo es invitar a cuestionar ciertas hipótesis en el análisis de factores tradicional. La SVD revela que los factores son inherentes a cualquier conjunto de datos estructurados matricialmente; lo crucial es cómo decaen los valores singulares. Los datos determinarán este decaimiento, con potenciales repercusiones teóricas profundamente transformadoras.
PALABRAS CLAVE
Descomposición en Valores Singulares, Análisis de Factores, Ciencias Humanas y Sociales.
ABSTRACT
The objects of study of the humanities and social sciences are intrinsically complex. Because it is philosophically attractive, and because it helps in practice to manage such complexity, one of the most influential central ideas throughout the history and present of these disciplines is the notion that the large number of empirical manifestations that characterize their objects of study are actually expressions of a few factors that influence all other variables. The corresponding statistical methodology to implement these ideas has different names and differs in detail in different disciplines, but one name that can be recognized in many of them is “factor analysis”. The first objective of this work is to present a classical method of linear algebra, known as “Singular Value Decomposition” (SVD), in an intuitive and at the same time rigorous way to the community of human and social sciences. SVD systematizes and generalizes the factorization of any data matrix. In addition, the method is of enormous importance in the era of big data and machine learning, which are increasingly influencing research in all areas of study. The second objective is to invite questioning of certain hypotheses in traditional factor analysis. The SVD reveals that factors are inherent in any matrix-structured data set; what is crucial is how singular values decay. Data will determine this decay, with potentially profoundly transformative theoretical repercussions.
KEYWORDS
Singular Value Decomposition, Factor Analysis, Humanities and Social Sciences.
Clasificación JEL: C02, C19, C63, C65
MSC2010: 5-01, 15A03, 15A04, 15A18, 15A60
1. Introducción
Los objetos de estudio de las ciencias humanas y sociales son intrínsecamente complejos. Porque es filosóficamente atractiva, y además porque ayuda en la práctica a manejar dicha complejidad, una de las ideas fuerza más influyente a lo largo de la historia de dichas disciplinas, es la noción de que la gran cantidad de manifestaciones empíricas que caracterizan sus objetos de estudio son en realidad expresiones de unos pocos factores que influyen sobre todas las demás variables.
La correspondiente metodología estadística para implementar esas ideas tiene diferente nombre en distintas disciplinas, y la implementación concreta también difiere en los detalles en diferentes disciplinas, pero un nombre que puede ser claramente reconocido en muchas de ellas es el análisis de factores (Harman, 1976).
El método surgió hace más de un siglo, originalmente en psicología, en los trabajos de Charles Spearman (1904; 1927), Cyril Burt (1909), Karl Pearson (1901), Godfrey H. Thomson (1938), J. C. Maxwell-Garnett (1919), Karl Holzinger (1930) y otros. Esos trabajos giraban alrededor de las ideas de Spearman, quien notando que diferentes tests que medían distintos tipos de habilidades relacionadas a la inteligencia tenían correlación positiva entre sí, concluyó que debía haber un factor central que influye en esas diversas capacidades cognitivas. A dicho factor lo llamó inteligencia general.
En estudios subsiguientes, para explicar mejor los datos, Spearman propuso su influyente “Teoría de los dos factores”, a los que llamó “inteligencia general” y “habilidad especial”. Además, desarrolló métodos matemáticos que le permitían encontrar relaciones lineales entre los resultados de los diferentes tipos de tests y esos factores subyacentes, que explicaban gran parte de la variabilidad de los mismos.
Eventualmente, con datos empíricos más detallados, comenzó a acumularse evidencia que sugería que hay en realidad más factores detrás de las habilidades que genéricamente llamamos inteligencia. Fue entonces natural que, con los resultados de varios tipos diferentes de tests para muchos individuos, la correspondiente matriz de correlaciones se analizara como objeto matemático a ser aproximado por matrices más sencillas, con un número relativamente pequeño de “factores” que explicaran la mayor parte posible de la variabilidad de los datos.
Fue Louis Leon Thurstone quien propuso el criterio del rango de la matriz de correlación como base para determinar el número de factores comunes (Thurstone, 1931; 1947) y formuló el problema en términos matriciales, lo que simplificó mucho el análisis posterior.
Concretamente, supongamos que dij es el resultado del test tipo j del i-ésimo individuo, donde hay n tipos de tests que se le toman a m individuos elegidos al azar en una población mucho mayor que m. Podemos ordenar dichos resultados en la matriz (1.1)
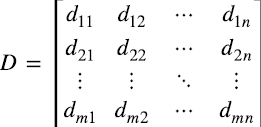
donde los elementos de la columna j se pueden pensar como muestras de una variable aleatoria representativa de las habilidades poblacionales medidas en el test tipo j. Restándole a dij la media de los resultados del tests j (1.2)
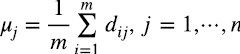
obtenemos la matriz “centrada” (1.3)
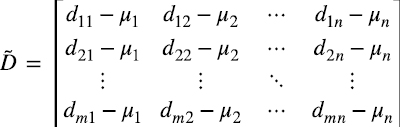
La estimación empírica de la desviación estándar σj es (1.4)
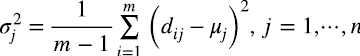
Las variables aleatorias zij=(dij-μj )/σj están normalizadas a varianza 1 con media cero. Pasamos entonces de la matriz D en (1.1), o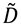 
en (1.3), a la matriz normalizada Z (1.5):
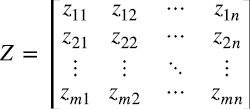
Spearman propone un modelo del tipo (1.6)
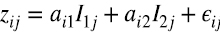
e interpreta a I1jcomo el impacto que tiene la “inteligencia general” en las habilidades medidas en el test j, a I2j como el impacto que tienen las “habilidades especiales” en las capacidades medidas en el test j, ail y ail, respectivamente, como la inteligencia general y habilidad especial del individuo i, y ϵij es el error asociado a la medición del test j para el individuo i. La expectativa de estos modelos es que ϵij tiendan a ser pequeños.
El modelo (1.6) se puede escribir matricialmente como (1.7)
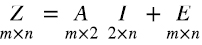
donde la primera fila de I corresponde a la inteligencia general y la segunda a las habilidades especiales. La matriz AI tiene rango 2, y representa la mejor aproximación de rango 2 de la matriz Z ya que los parámetros se elegían de modo de minimizar la suma de los cuadrados de los errores.
En un modelo de k factores, la matriz A tiene dimensiones m x k y la matriz I dimensiones k x n, con las k filas de A linealmente independientes y lo mismo para las k columnas de I. En ese caso la matriz AI tiene rango k, y representa la mejor aproximación de rango k de la matriz Z.
Muchos años más tarde, en finanzas, para entender los mercados de capitales, se replicó el mismo patrón: primero se propuso una teoría de un factor, para luego concluir que varios factores explican mejor los datos. El celebrado CAPM (Capital Assets Pricing Model) es un modelo de un factor (Sharpe, 1964; Lintner, 1975; Mossin, 1966) para predecir el retorno esperado de activos de riesgo en un mercado de capitales en equilibrio. Ameritó el premio Nobel de Economía para William Forsyth Sharpe en 1990 (compartido con Harry Markowitz y Merton Miller).
El modelo se generalizó a modelos de varios factores, por ejemplo en la popular “Teoría de arbitraje de precios” (Arbitrage pricing theory) de Stephen A. Ross (2013) y otros modelos multifactoriales de Riesgo y Retorno. Tanto el CAPM como los modelos de varios factores forman parte de la formación estándar en maestrías y doctorados con especialidad en finanzas.
En macroeconomía, por ejemplo, en la literatura sobre el ciclo económico real (RBC, o “real business cycle”) y el equilibrio general estocástico dinámico (DSGE o “Dynamic stochastic general equilibrium”), típicamente se modelan unos pocos tipos de perturbaciones (factores) que afectan a todas las variables como pueden ser productividad, demanda, oferta, etc. (Stock y Watson, 2011 y 2015; Bai-Ng, 2002 y 2008).
No es una exageración decir que esencialmente todas las ciencias humanas y sociales han utilizado, y siguen utilizando, modelos de factores. Las razones se mencionaron antes, pero vale la pena enfatizarlas. Por un lado, la idea de que unos pocos factores explican muchos datos empíricos es filosóficamente atractiva. Por el otro, es computacionalmente mucho más manejable: mientras que la matriz Z tiene m x n elementos, el producto AI tiene (m + n) x k elementos, lo cual es una gran ventaja si k ≪ n.
A la luz de la importancia que tiene el análisis de factores en ciencias humanas y sociales, es un poco sorprendente que un método clásico de álgebra lineal conocido como “la Descomposición en valores singulares” (SVD), que sistematiza y generaliza la descomposición en factores de cualquier matriz, y que constituye un tema estándar en cursos de posgrado en matemática aplicada, no sea parte de la formación estándar en las mencionadas disciplinas. Si bien su uso en estas disciplinas muestra una pendiente fuertemente creciente (Athey et al, 2017; Athey e Imbens, 2019 y referencias en dichos trabajos), en la opinión del autor, entenderlo y manejarlo con destreza sería de gran importancia para cualquier investigador en estas áreas por al menos dos razones.
Por un lado, como se mencionó, este método automatiza y generaliza en muchas direcciones el análisis de factores.
Si el interés pasa por una matriz con un claro significado estadístico, como lo tienen la matriz D en (1.1), o en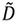 
(1.3), o la matriz Z en (1.5), veremos que la matriz varianza-covarianza es 
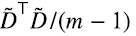, y la matriz de correlaciones es Z⊤Z/(n-1). Aplicando SVD a estas matrices, que por características específicas de las mismas que se explicarán más adelante, lleva el nombre de “análisis de componentes principales”, uno obtiene automáticamente el análisis completo de factores de las correspondientes distribuciones.
Como la matriz original D en (1.1) fue generada a partir de n datos para cada uno de m individuos, es natural pensar en dichos datos como m vectores en un espacio vectorial de n dimensiones. Entonces, en esos casos, al análisis estadístico se le suma uno geométrico: el análisis de factores se reduce a aproximar esa “nube” de datos en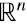 
por sus proyecciones en el “mejor” hiperplano de k dimensiones.
Pero hay muchos ejemplos de datos en los que no hay una diferenciación clara de significado entre filas y columnas, como sí lo hay en la matriz D, ni hay un correspondiente significado estadístico de los datos. Por ejemplo, imaginemos en una economía una matriz en la que tanto las filas como las columnas representan personas humanas y jurídicas, y el elemento ij de la matriz representa alguna medida de cuánto comercian entre sí la persona i con la persona j. Como SVD funciona para cualquier matriz, con SVD tiene sentido pensar en factores aún para matrices como esta. Más aún, la existencia misma de la macroeconomía como disciplina, con sus modelos basados en relativamente pocas variables como trabajo, capital, productividad, inflación, etc., depende de que dicha matriz tenga, y mantenga a lo largo del tiempo, un muy bajo “rango efectivo”.
Una segunda razón para familiarizarse con SVD es que, debido en parte a algoritmos extremadamente optimizados para implementarlo, el método es de enorme importancia en la era de big data y machine learning, que influyen de manera creciente en la investigación en todas las áreas de estudio, y las ciencias humanas y sociales no son la excepción.
Por ejemplo, en aplicaciones de procesamiento de imágenes, como en el cálculo de “autocaras” (Eigenfaces) para proporcionar una representación eficiente de imágenes faciales en el reconocimiento facial (Muller et al., 2004; Turk y Pentland; 1991a y 1991b).
También en genómica (Alter et al., 2000; Holter et al., 2000). En un sorprendente trabajo, Novembre, Johnson, Bryc et al. (2008), literalmente reproducen el mapa de Europa a partir de los dos factores principales en los vectores genéticos caracterizando las mutaciones de 3000 individuos europeos. Esto es especialmente sorprendente cuando uno observa que dichos vectores “viven” en más de medio millón de dimensiones.
Tal vez más sorprendente son los trabajos de procesamiento de lenguaje natural (Deerwester et al., 1990). En trabajos recientes basados en matrices de co-ocurrencia de palabras, donde el elemento ij de la matriz cuenta la cantidad de veces que las palabras i y j ocurren en un texto a menos de d palabras entre sí (por lo tanto la matriz es simétrica), siendo esos textos, por ejemplo, artículos de Google News, SVD descubre sorprendentes estructuras semántica y sintáctica en subespacios de relativamente baja dimensión (en dimensión 100 por ejemplo, cuando las palabras “viven” en ∼ 10.000 dimensiones). Además, ha servido para detectar sesgos en dichos textos, y desarrollar algoritmos para quitarle dichos sesgos. Esto es especialmente importante dado que tales algoritmos son usados por empresas para preseleccionar curriculum vitae de manera automática (Bolukbasi et al., 2016).
SVD también muestra su poder para completar bases con datos faltantes, donde el objetivo es proporcionar la mejor predicción posible de lo que deberían ser esas entradas, ver por ejemplo (Athey et al., 2017; Athey e Imbens, 2019).
1.1 ¿Qué es SVD?
El teorema fundamental establece que cualquier matriz A de dimensiones m x n se puede expresar como el producto de tres matrices (1.8):
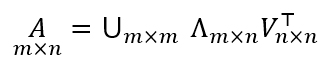
donde las matrices U y V son ortogonales (matrices cuadradas cuyas filas y columnas son vectores ortonormales), el superíndice “ ⊤ “ indica traspuesta si la matriz es real y traspuesta conjugada si la matriz es compleja, y la matriz Λ es diagonal y semidefinida positiva. Es decir, los elementos no diagonales de Λ son todos cero, y los elementos de la diagonal principal λi son, o bien positivos, o cero, con tantos valores no nulos como rango k tenga la matriz A. Los elementos diagonales de Λ generalmente se ordenan de mayor a menor λ1 ≥ λ2 ≥ ... ≥ λn . Es decir, asumiendo que n ≥ m, en cuyo caso necesariamente k < n, (1.9) (1.10)
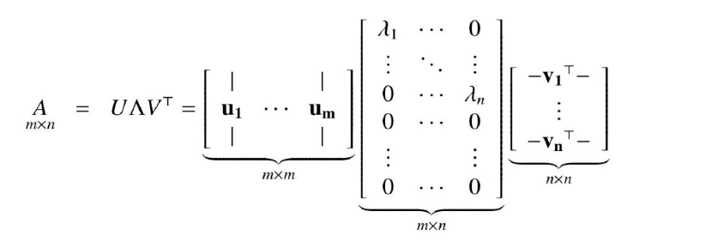
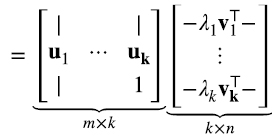
donde la segunda igualdad se deriva trivialmente de la primera asumiendo que λi = 0 para i = k + 1,..., n.
La forma (1.10) de la descomposición SVD es idéntica a la forma (1.7) utilizada en análisis de factores y descartando la matriz de errores E, pero la forma (1.9) es la fundamental. De hecho, (1.10) no es la única manera de darle a A la forma (1.7). Por ejemplo, los valores singulares λi pueden multiplicar a las respectivas columnas de U en vez de las filas de V⊤, y cualquier combinación entre ambas también funciona.
La implementación de SVD en las librerías de software es estándar y tremendamente optimizada. Por ejemplo, en Matlab, escribiendo [U, L, V] = svd (A). Matlab devuelve las matrices U, L y V correspondientes a (1.9). Lo mismo ocurre con la librería linalg de numpy en Python, donde escribiendo U, s, VT = np. linalg.svd(A, full_matrices = False). Python devuelve las matrices U,V⊤, y s, que es un vector con los elementos diagonales de Λ.
Si uno quiere aproximar una matriz A de rango k con una matriz de rango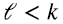 
, la mejor aproximación de rango 
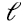consiste simplemente reemplazar por cero en (1.9) o (1.10) los valores singulares λi, para 
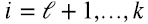. “Mejor aproximación” en el sentido de la norma de Frobenius (1.11):
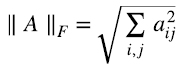
Es decir, para toda otra matriz B de rango k, (1.12)
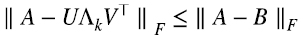
donde Λk es Λ en (1.9) con los valores singulares más chicos,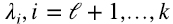 
, reemplazados por cero, Eckart y Young (1936).
La elección del rango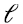 
de la aproximación deseada depende del usuario, es decir, 
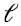es un parámetro exógeno en el método SVD.
El tiempo de ejecución de SVD escala rápido, como el menor de O(m2n) y O(n2m), por lo que una típica computadora portátil puede calcular el SVD de una matriz de 5000 x 5000 sin problemas, pero se le complica con una matriz de 10.000 x 10.000. Si uno se contenta con los mayores k valores singulares, como es usualmente el caso cuando uno busca la mejor aproximación de la matriz en k factores en lugar la descomposición completa, el tiempo de ejecución de SVD escala como O(mnk), lo cual es una enorme ventaja si k ≪ m, n Además, para matrices especiales (como es el caso en la mayoría de las aplicaciones) hay algoritmos mucho más rápidos (Liberty et al., 2007).
Este trabajo tiene dos objetivos. Por un lado, presentar a la comunidad de ciencias humanas y sociales un método sistemático, conocido como la “Descomposición en valores singulares” (SVD), para descomponer cualquier matriz en factores. Aunque un mínimo de conocimiento de álgebra lineal se asume, el camino elegido tiene como sub-objetivo familiarizar aún más a la comunidad mencionada con métodos de álgebra lineal, de enorme y creciente importancia en la era de Big Data, y además permite introducir SVD de manera natural, donde el lector casi que va adivinando la forma antes de leerla.
El segundo objetivo, que desarrollaremos en la conclusión cuando se haya entendido el método, es invitar a cuestionar ciertas hipótesis subyacentes en el uso tradicional del análisis de factores en estas disciplinas. En la opinión del autor, la naturaleza misma de SVD, y los sorprendentes resultados de numerosas aplicaciones recientes, una minúscula parte de las cuales fueron mencionadas más arriba, ameritan una revisión crítica de tales hipótesis.
El resto del trabajo se organiza de siguiente manera: en la siguiente sección definimos la notación que vamos a utilizar y recordamos algunos elementos básicos de álgebra lineal que se asumen conocidos, en la sección 3 recordamos las relación biyectiva entre matrices y transformaciones lineales y derivamos de manera simple la igualdad entre en “rango por fila” y “rango por columna” de cualquier matriz, en la sección 4 definimos el producto “outer” entre vectores, que suele no cubrirse en cursos básicos de álgebra lineal y resulta fundamental para entender SVD de manera intuitiva, en la sección 5 derivamos SVD, en la sección 6 clarificamos la relación entre SVD, el análisis de factores y el análisis de componentes principales. Finalmente, en la sección 7 resumimos el trabajo y, como mencionamos antes, analizamos ciertas hipótesis subyacentes en el uso tradicional del análisis de factores en estas disciplinas, invitando a una revisión crítica de tales hipótesis.
2. Notación
Se usa letras minúsculas en negrita “v” para vectores, letras minúsculas “a” para escalares, y mayúsculas “A” para matrices. A menos que se especifique lo contrario los vectores son “columna”, y si queremos referirnos a vectores “fila” lo hacemos explícitamente con el símbolo de traspuesto v⊤.
A los vectores de la base “canónica” la denotamos êi,n , donde n es la dimensión del espacio vectorial subyacente. Por ejemplo, en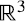 
tenemos (2.1):
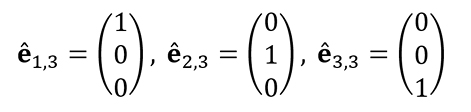
Vamos a usar la notación matricial v⊤w para el producto escalar entre vectores, a los que pensamos como matrices n x 1. Por ejemplo, para vectores en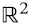 
(2.2):
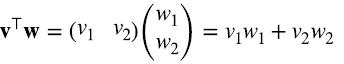
Con el producto escalar definimos la “norma”, o magnitud, o longitud de vectores como (2.3)
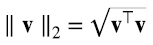
y la distancia entre dos vectores v e w como ∥ v - w ∥2.
Con el producto escalar (2.2) el ángulo θ entre dos vectores v y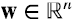 
es el ángulo que tiene por coseno (2.4)
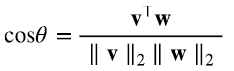
De (2.3) vemos que v/ ∥ v ∥2 y w/ ∥ w ∥2 tienen norma 1. Si el producto escalar entre dos vectores es cero, cos θ = 0 , es decir θ es π/2 o 3π/2, y los vectores son ortogonales (o perpendiculares).
Si v tiene norma 1,v⊤w es la proyección de w en la dirección de v, y (v⊤w)v es un vector que apunta en la dirección de v y su norma es el valor absoluto de la proyección de w en la dirección de v.
Dada una matriz real A “cuadrada”, es decir, 
, la misma es simétrica si el elemento aij = aj, es decir, si A⊤ = A. Una matriz cuadrada genérica de n x n tiene n2 elementos independientes. Si es simétrica, tenemos los n elementos de la diagonal por un lado, y de los restantes n2 - n = n(n - 1) elementos, solo la mitad son independientes. Entonces hay n + n(n - 1) /2 = n(n + 1)/2 elementos independientes.
Dada una matriz cuadrada A, un vector vi no nulo se llama “autovector” (o vector propio), y un escalar λi es el correspondiente “autovalor” (o valor propio), si satisfacen la siguiente ecuación (2.5)
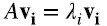
Todas las librerías de software numérico tienen funciones que calculan autovalores y autovectores.
Para una matriz real cuadrada genérica A, en general, tanto los autovalores como las coordenadas de los autovectores son números complejos. Pero si la matriz es simétrica resulta que varias propiedades se satisfacen:
1.Tanto los autovalores como las coordenadas de los autovectores son números reales.
2.Si la matriz es de n x n, hay exactamente n autovalores y n autovectores (si dos o más autovalores son iguales esto sigue valiendo con ciertas aclaraciones, pero son irrelevantes para nuestros propósitos.)
3.Los autovectores (o vectores propios), pueden elegirse ortogonales entre sí, y de norma 1. Es decir, si vi y vj son dos autovectores diferentes, entonces vi⊤vj = 0 , y vi⊤vi = 1.
3. Rango por filas y por columnas de una matriz
Un resultado clásico de álgebra lineal es que para cualquier matriz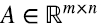 
, el número de filas linealmente independientes es igual al número de columnas linealmente independientes.
El número de filas linealmente independientes se conoce como “rango por filas”, y el número de columnas linealmente independientes se conoce como “rango por columnas”. Entonces, otra manera de presentar el resultado mencionado en el párrafo anterior es:
rango por filas de A = rango por columnas de A ≡ rango de A
Si la matriz A multiplica por izquierda a un vector 
, devuelve un vector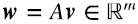 
. Más generalmente, una matriz A se puede pensar como una función lineal que transforma un vector v perteneciente a un espacio vectorial V en otro vector w perteneciente a un espacio vectorial W.
Figura 1. dimV = dimV1 + dimV2, y dimV1 = dimW
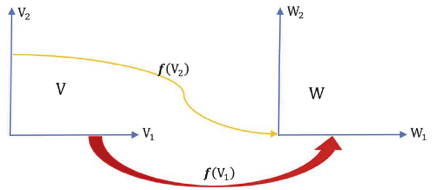
Fuente: Elaboración propia.
Consideremos el conjunto V2 ⊂ V tal que si v2 ∈ V2, A(v2) = 0 , ver figura 1. V2 es un subespacio vectorial de v (si v2,a y v2,b ∈ V2, la linealidad del producto matriz por vector implica A(aav2,a + abv2,b) = 0, por lo que αav2,a + αbv2,b) ∈ V2. V2 se conoce como espacio nulo de A, o N(A).
Todo elemento v ∈ V se puede expresar de manera única de la forma v = v1 + v2, donde v1 pertenece al complemento ortogonal de V2, al que llamamos V1, y v2 ∈ V2. En general, en un espacio con producto escalar, el complemento ortogonal de un subespacio es también un subespacio. Se dice que v es la “suma directa” de V1 y V2,V = V1 ⊕ V2,V1 ∩ V2 ={0}, y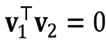 
.
Ya sabemos que la imagen de V2 es {0}, consideremos ahora la imagen de V1, a la que llamamos W1 ⊂ W, ver Figura 1, es decir, (3.2)
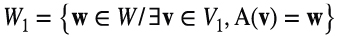
Un resultado estándar de álgebra lineal es, (3.3)
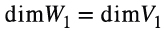
Por más información sobre este resultado, ver por ejemplo D. C. Lay (2007).
Para ver la implicancia de este resultado conviene recordar dos maneras diferentes de mirar el producto matriz por vector. La primera es mirando a la matriz como un conjunto de filas (3.4):
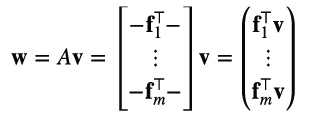
cada componente es el producto escalar del correspondiente vector fila de A con v.
Vimos que todo elemento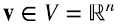 
se puede expresar de manera única de la forma v = v1 + v2, donde v1 ∈ V1, v2 ∈ V1 = N(A) es el espacio nulo de A, y v1⊤v2 = 0. La expresión (3.4) hace explícito que para todo elemento v2 ∈ V2 = N(A), Av2 = 0, si y solo si fi⊤v2 = 0 para todo i = 1,..., m. Es decir, v2es ortogonal a los vectores cuyos transpuestos son las filas de A, por lo que V1 es el subespacio de 
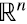linealmente dependiente de dichos vectores y V2 es el subespacio de 
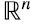ortogonal a V1. El rango por fila de A es entonces la dimensión de V1.
La segunda manera de mirar al producto matriz por vector es mirando a la matriz como un conjunto de columnas (3.5):
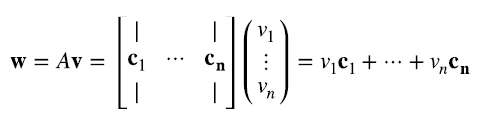
El resultado es una combinación lineal de los vectores columna de A con coeficientes iguales a las componentes de v. El rango por columna de A, es decir, el número de columnas de A linealmente independientes, es entonces la dimensión de W1, ver Figura 1.
Pero como mencionamos, dimW1 = dimW1 , por lo que el rango por columna deA =rango por fila deA =rangodeA. Es decir, el subespacio de todas las combinaciones lineales de las filas de A tiene igual dimension que el subespacio de todas las combinaciones lineales de las columnas de A . O, equivalentemente, el número de filas linealmente independiente es igual al número de columnas linealmente independientes, independientemente de cuánto sea m y n. Este resultado no es del todo intuitivo a partir de lo visto hasta este punto. Se volverá intuitivo cuando veamos una tercera manera de mirar a las matrices: como suma de productos “outer”, el tema de la siguiente sección.
4. Producto “outer”
Llamamos producto “outer” entre un vector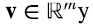 
otro vector 
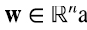(4.1)
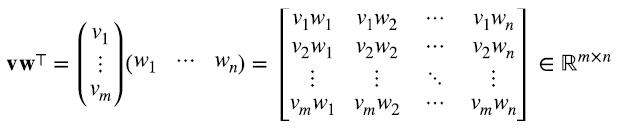
Es decir, el producto outer es simplemente el producto matricial entre la matriz m x l asociada al vector v y la matriz l x n asociada al vector w⊤, siendo el resultado una matriz de m x n de rango igual a 1.
Por ejemplo, (4.2)
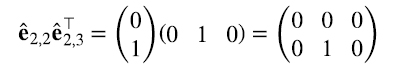
Siguiendo con este ejemplo, queda claro que cualquier matriz A de 2 x 3 puede escribirse como una combinación lineal de productos outer de las correspondientes bases canónicas (4.3):
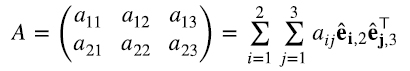
En general, si êi,m, i = 1,...,m, denotan a los vectores de la base canónica en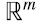 
y êj,n, j = 1,...,n, a los vectores de la base canónica en 
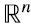, cualquier matriz A de m x n puede escribirse como una combinación lineal de productos outer de las correspondientes bases canónicas (4.4):
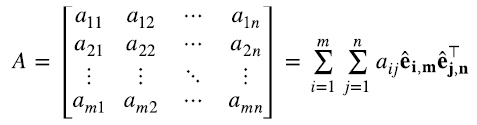
La matriz A se puede escribir de infinitas maneras diferentes como combinación lineal de productos outer. Nos enfocamos en dos.
Mirando a la matriz A como un conjunto de n vectores columna, cada uno en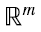 
(4.5)
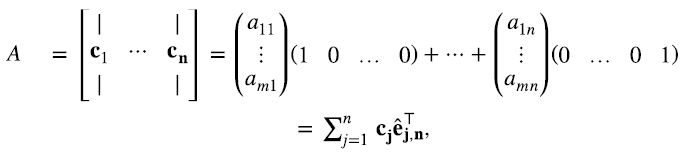
donde (cj)i = aij. Es decir, el elemento i del vector columna j es (cj)i = aij.
De manera análoga, mirándola como un conjunto m vectores, cada uno en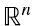 
, cuyos transpuestos corresponden a las filas de A (4.6):
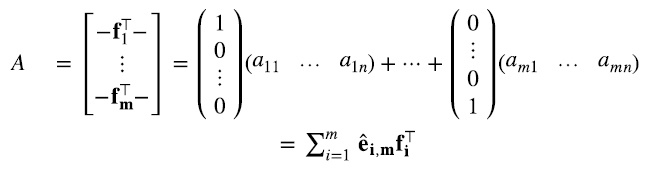
donde (fi⊤)j =aij. Es decir, el elemento j del vector fila i es (fi⊤)j =aij.
Veamos el efecto de multiplicar por derecha un vector columna por el producto outer entre dos vectores (asumimos que las dimensiones son correctas) (4.7):
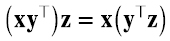
Como todo producto matricial, el producto outer satisface la propiedad asociativa. La última igualdad, sin embargo, tiene gran utilidad, porque el producto escalar entre y y z va a ser cero si esos vectores son ortogonales. Es decir que el efecto de la matriz xy⊤ sobre el vector z es multiplicar escalarmente a z por y y al escalar resultante multiplicarlo por el vector x. El resultado tiene la dirección de x. Por lo tanto, si y = x y ∥ x ∥ = 1,xx⊤ es un proyector en el subespacio generado por x.
De la misma manera, multiplicando por izquierda un vector fila por el producto outer entre dos vectores (nuevamente asumimos que las dimensiones son correctas) es (4.8):
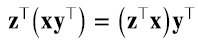
Además de la propiedad asociativa por derecha y por izquierda, es fácil ver que el producto outer satisface las siguientes propiedades (4.9):
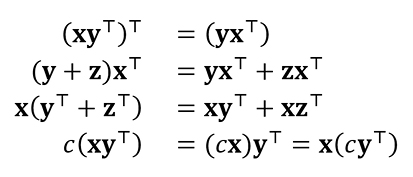
Prometimos en la sección anterior que el hecho de que hay igual número de filas y columnas linealmente independientes, o, equivalentemente, que dimV1 = dimW1, se volvería intuitivo con productos outer. Veremos ahora que las propiedades (4.9) es todo lo que necesitamos para convencernos de este resultado.
Supongamos que el rango por fila de la matriz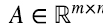 
es k. Claramente k ≤ n porque las filas de A son vectores en 
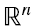transpuestos, y hay como máximo n vectores linealmente independientes en 
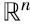. Además k ≤ m porque hay solo m filas.
Mirando a la matriz A en la forma (4.6), supongamos, sin pérdida de generalidad, que las primeras k filas son linealmente independientes y las filas k + 1,..., n son linealmente dependientes de las primeras k, es decir (4.10)
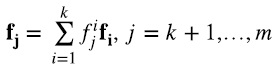
donde los escalares fji, i = 1,..., k, j = k + 1,..., m son únicos. Entonces, de (4.6) (4.11)
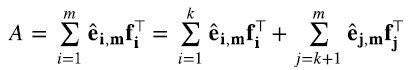
Insertando (4.10) en el último término de (4.11), y usando las propiedades (4.9) del producto outer (4.12)
(4.12)
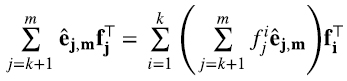
Reemplazando esta expresión en (4.11), usando nuevamente las propiedades (4.9), (4.13)
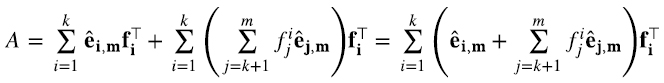
En esta última expresión es una suma de k productos outer. Por hipótesis, los vectores fi son linealmente independientes, y los vectores (4.14)
obviamente también lo son, ya que los êi,m son los primeros k vectores de la base canónica de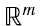 
. Entonces, en (4.13) logramos expresar a la matriz A como una suma de k productos outer (es decir de k matrices de rango uno) de la forma (4.15)
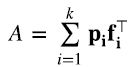
donde los k vectores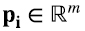 
son linealmente independientes y los k vectores 
también lo son. (4.15) inmediatamente implica que dimV1 = dimW1. Por hipótesis sabemos que dimV1 = k, y para todo vector 
(4.16),
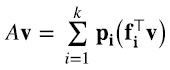
es una combinación lineal de los k vectores pi. Variando v en V1 podemos hacer que los k productos escalares fj⊤v,i =1,..., k, adquieran cualquier valor deseado, por lo que cubrimos toda posible combinación lineal de los k vectores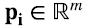 
. Como los pi son linealmente independientes, se sigue que dimW1 también es k.
Un argumento análogo muestra que si tenemos k columnas de A linealmente independientes, entonces tiene que haber k filas linealmente independientes, o, que si dim W1 = k, entonces dimV1 = k.
Finalizamos esta sección expresando el producto de matrices en términos de productos outer. Supongamos que la matriz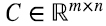 
es el producto de la matriz 
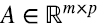por la matriz 
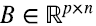. Entonces, el elemento ij de C es (4.17)
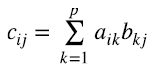
Consideremos, por ejemplo, el elemento k = 2 en la suma en (4.17): ai2b2j. Es el elemento i-ésimo de la columna 2 de la matriz A, multiplicado por el elemento j-ésimo de la fila 2 de la matriz B. Esto, a su vez, se puede pensar como el elemento ij del producto outer entre el vector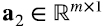 
correspondiente a la segunda columna de A y el vector 
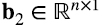, cuyo transpuesto es la fila 2 de la matriz B. En otras palabras, (a2b2⊤)ij = ai2b2j. Entonces, la suma en (4.17), expresada en términos de productos outer, es (4.18)
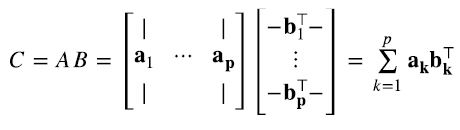
5. Descomposición en valores singulares
Como vimos, la expresión (4.15), válida para cualquier matriz A de rango k, inmediatamente implica que dimV1 = dimW1. Como veremos, la descomposición en valores singulares simplemente requiere probar que A se puede escribir como la suma k productos outer donde, además, los k vectore {pi} y los k vectores {fi} se pueden elegir simultáneamente ortonormales. Empecemos el análisis con matrices de 2 x 2.
En la figura 2 vemos que generando una matriz D al azar, las matrices simétricas y semidefinidas positivas DD⊤ DD^⊤ y D⊤D tienen obviamente autovectores ortogonales, pero no es obvia la relación entre ellos, como se ve en las diferentes figuras. Sin embargo, los autovalores de ambas matrices siempre son iguales. Tratemos de entender por qué esto es así.
DD⊤ es simétrica, ya que (DD⊤) = (D⊤)⊤D⊤ = DD⊤, por lo que sus autovalores son reales y sus autovectores son reales ortogonales. Además, dado cualquier vector v, la norma al cuadrado de w = D⊤v es w⊤w = v⊤DD⊤v ≥ 0, por lo que DD⊤ es semidefinida positiva. Mismas conclusiones valen para D⊤D.
Figura 2. Matriz D generada al azar con valores surgidos de una normal N(0,1)(D = np.random.randn(2,2) en Python numpy.)
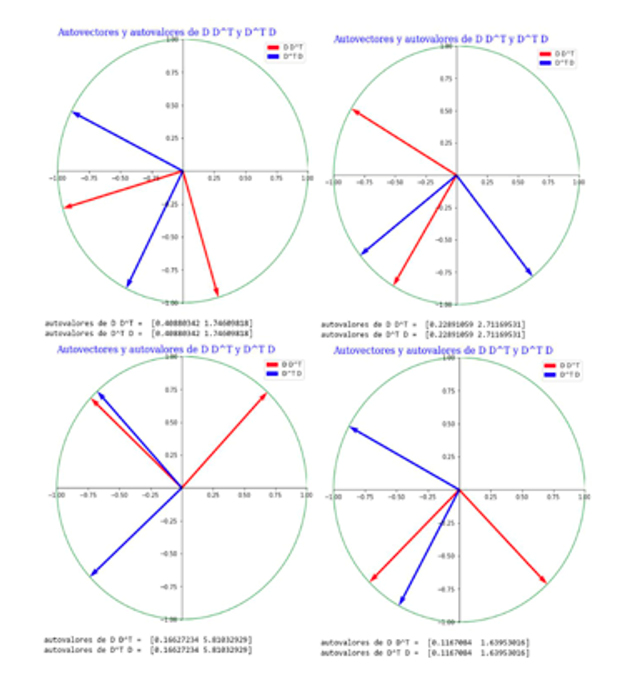
Fuente: Elaboración propia.
Nota: Las matrices simétricas y semidefinidas positivas DD⊤ y D⊤D tienen autovectores ortogonales, pero no obvia relación entre ellos, como se ve en las diferentes figuras. Sin embargo, los autovalores de ambas matrices siempre son iguales.
Los autovectores y autovalores de DD⊤ y D⊤D satisfacen las siguientes ecuaciones (5.1) (5.2)
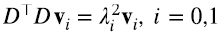
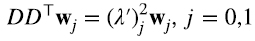
Escribimos los autovalores como el cuadrado de un número real porque sabemos que son no negativos. La Figura 2 indica que, aunque generamos las matrices D al azar, podemos ordenar los autovalores de D⊤D y DD⊤ de modo que λi2 = (λ’)i2. ¿Cómo podemos entender esto? Consideremos por ejemplo (5.2), y multipliquemos por izquierda por D⊤ (5.3):
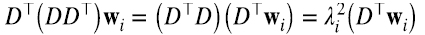
comparando (5.3) con (5.1) e identificando a vi con D⊤ wi, explicamos por qué λi2 = (λ’)i2 y además descubrimos una relación entre los autovectores de ambas matrices que no era obvia desde la figura 2 (5.4):
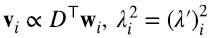
Ponemos el signo de proporcionalidad y no el de igualdad porque nada asegura que D⊤ wi esté normalizado a uno si wi lo está.
De la misma manera, multiplicando con D por izquierda a (5.1) llegamos a la conclusión de que (5.5)
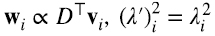
Acabamos de encontrar una relación interesante entre los autovectores de DD⊤ y D⊤D. Como mencionamos, estas matrices son simétricas, por lo que sus autovectores normalizados a uno forman bases ortonormales de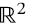 
. Además, son semidefinidas positivas, es decir, sus autovalores son positivos o cero (5.6) (5.7).
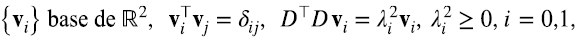
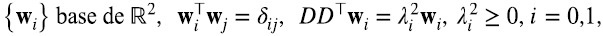
esto significa que admiten la siguiente descripción en términos de productos outer (5.8) (5.9):
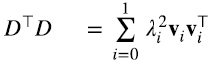
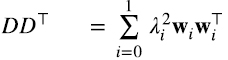
Por ejemplo, los autovectores y autovalores determinan unívocamente a la matriz D⊤D, y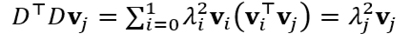 
Mirando las expresiones (5.8-5.9) resulta casi obvio que D y D⊤ se pueden escribir así (5.10) (5.11):
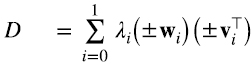
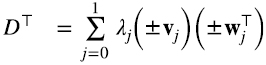
donde λi es la raíz real no negativa del número real no negativo λi2. La restricción de que los vectores de las bases {vi} y {wi} en (5.6-5.7) estén normalizados a 1 deja ambiguo un signo ±1, pero alguna de las 22 = 4 combinaciones tiene que ser correcta. Sean cuales sean los signos correctos (5.12),
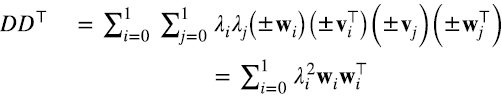
recuperamos (5.9). En (5.12) usamos la propiedad asociativa y (±vi⊤) (±vj) = 1 si i = j, o 0 si i ≠ j. Lo mismo vale para D⊤D.
A partir las expresiones (5.8-5.9) obtuvimos 5.10-5.11) con una ambigüedad de signo, pero, independientemente del signo, a partir de (5.10-5.11) recuperamos (5.8-5.9). Esto indica que podemos elegir el signo de los autovectores {wi} de DD⊤ y {vi} de D⊤D de modo que (5.13) (5.14)
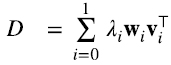
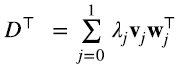
Como indicamos en el comienzo de esta sección, expresiones (5.13-5.14) era lo que buscábamos, son análogas a (4.15), pero con {pi} y {fi}ortogonales. (5.13) y (5.14) son la descomposición en valores singulares de las matrices D y D⊤ respectivamente.
A pesar de que fue derivado para matrices de 2 x 2, todas las operaciones realizadas valen para matrices reales de cualquier dimension finita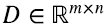 
. En ese caso 
mientras que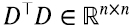 
. Pero como vimos en la sección 3 en general, y en la sección 5 en términos de productos outer, dimW1 = dimV1, o el número de filas linealmente independiente es igual al número de columnas linealmente independientes, independientemente de cuánto sea m y n. Esto implica que si,por ejemplo, n ≤ m, DD⊤ va a tener el menos m - n autovalores nulos y las expresiones (5.13-5.14) siguen valiendo incluyendo en la suma solo los “valores singulares” λi no nulos.
En libros de texto, y en librerías de software como linalg de numpy, la descomposición en valores singulares de una matriz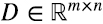 
suele presentarse indicando que la matriz D se puede escribir como (5.15)
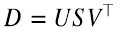
donde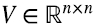 
, con sus columnas dadas por los vectores ortonormales vi, de modo que las filas de V⊤ son 
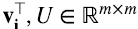con sus columnas dadas por los vectores ortonormales wi, y 
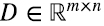con los elementos de la diagonal principal iguales a los valores singulares positivos λi y todos los demás elementos iguales a cero.
Es fácil ver que la expresión (5.15) es equivalente a (5.13). Recordando la ecuación (4.18) para productos de matrices, asumiendo que el rango de D es p, (5.15) implica (5.16):
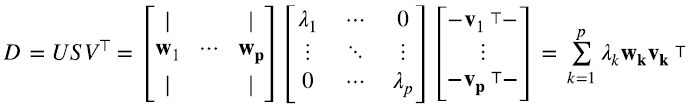
Finalizamos esta sección notando que si bien la descomposición en valores singulares vale para cualquier matriz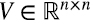 
, en la práctica es especialmente útil cuando relativamente pocos valores singulares λi son mucho mayores que el resto. Supongamos por ejemplo que, como ocurre en (5.16), el rango de D es p pero los primeros s ≪ p valores principales son mucho mayores el resto, en ese caso, para muchas aplicaciones (5.17),
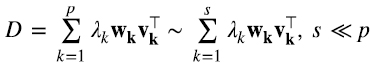
suele ser una excelente aproximación de D y mucho más fácil de analizar.
Como fue adelantado en la introducción, se puede probar que (5.16) es la mejor aproximación de la matriz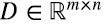 
de rango p con matrices de rango s, en el sentido de que minimiza la “distancia Euclidiana” en el espacio de las matrices de 
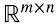(o norma de Frobenius) (5.18):
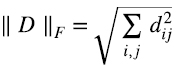
Es decir, para toda otra matriz B de rango s (5.19),
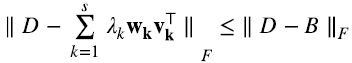
Aunque esta sección pretende ser autocontenida, para el lector interesado, Stewart (1993) es una referencia interesante sobre la historia de la SVD.
6. Relación entre SVD, análisis de componentes principales y análisis de factores
Antes de atacar de manera directa el tema de esta sección, es conveniente entender qué pasa con SVD cuando se aplica a matrices simétricas.
Recordemos que en la introducción vimos que para una matriz real cuadrada y simétrica A, los autovectores, y autovalores (6.1)
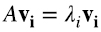
son reales, hay n de ellos, y se pueden elegir ortonormales (6.2) (6.3):
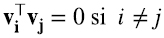
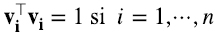
Comparando esto con la última igualdad en (5.16), notamos que para el caso de matrices reales y simétricas, los vectores singulares por derecha vi y por izquierda wi tienen que ser iguales entre sí e iguales a los autovectores vi, y los valores singulares λi tienen que ser los autovalores de A. Es decir, A se tiene que poder escribir como (6.4)
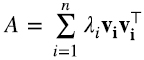
de modo que cuando actúa sobre un autovector vj tenemos (6.5)
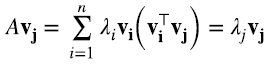
donde en la última igualdad usamos (6.2-6.3). Como el producto matriz por vector es lineal, la validez de (6.4) para los n autovectores linealmente independientes vi asegura que dicha expresión vale en general.
La expresión (6.4) es muy parecida a las ecuaciones (5.8-5.9), pero en estas últimas expresiones λi2 nunca es negativo, mientras que los autovalores de A en (6.4) pueden ser negativos: que A sea simétrica asegura que los λi sean reales, pero pueden ser negativos.
Pero parte de la definición de SVD en (5.16) es que los λi sean no negativos. Esto se arregla muy fácilmente: supongamos que en la expresion (6.4) el sumando k-ésimo tiene λk negativo, entonces, simplemente cambiándoles el signo a λk y a un vk tenemos (6.6):
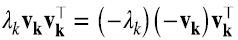
donde -λk es positivo. Si hacemos esto con todos los autovalores negativos recuperamos la expresión SVD en (5.16), que si bien demandaba que los λk sean positivos, no demandaba que los vectores singulares por derecha y por izquierda sean iguales.
En cualquier caso, si vi es un autovector de A, - vj también es un autovector de A con el mismo autovalor, linealmente dependiente de vi, es decir, está en el mismo subespacio lineal que vi. Como se verá en unas líneas, esto habilita una interpretación geométrica muy útil de SVD para el caso en que la matriz A es cuadrada n x n y simétrica: la mejor aproximación de rango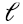 
de la matriz A es la proyección ortogonal de los vectores columna (o fila, es indistinto) que viven en 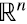sobre el “mejor” subespacio de dimensión 
.
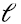Resumiendo, para matrices simétricas, en la expresión general (5.16) de SVD, los vectores singulares por derecha e izquierda correspondientes a autovalores no negativos son iguales entre sí e iguales a los autovectores de la matriz, y los vectores singulares por derecha e izquierda correspondientes a autovalores negativos también son autovectores de la matriz, pero difieren entre sí en un signo menos.
Como vimos en la introducción, en análisis de factores en las ciencias humanas y sociales, típicamente tenemos una matriz D de datos empíricos donde, retomando el ejemplo usado en esa sección, el elemento dij es el resultado del test tipo j del i-ésimo individuo, hay n tipos de tests que se le toman a m individuos elegidos al azar en una población mucho mayor que m. A partir de D obtenemos la matriz “centrada”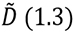 
restándole a cada elemento dij la media μj de los resultados del tests j. Y, dependiendo de la aplicación, normalizábamos las columnas a varianza 1 obteniendo la matriz Z en (1.5), para finalmente realizar el análisis de factores de dicha matriz.
Este último paso no siempre se realiza, porque los diferentes valores de las varianzas de las variables aleatorias muchas veces es parte importante de la señal que queremos capturar, y en lo que sigue suponemos que no normalizamos las columnas a varianza 1. En cualquier caso, todo lo que sigue continúa valiendo si decidiéramos normalizarlas.
Recordemos (1.4) para la estimación empírica de la desviación estándar σj (6.7)
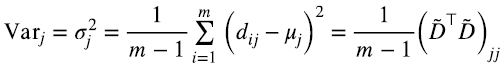
y la estimación empírica de la covarianza es (6.8)
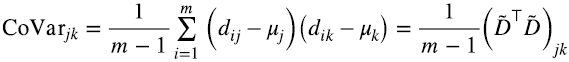
Es decir, toda la información estadística de segundo orden está encapsulada en la matriz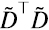 
. Pero vimos en la sección 5 que una matriz de la forma 
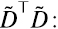a) es cuadrada, b) es simétrica, y c) es semi-definida positiva. Es decir, sus autovalores nunca son negativos.
Más aún, la manera como la derivamos hizo explícito que si la SVD de la matriz 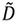es (6.9)
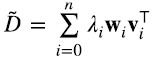
la SVD de la matriz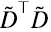 
es (6.10)
Es decir, los vectores singulares por derecha de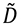 
son los autovectores de la matriz varianza-covarianza, y si λi es un valor singular de 
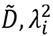es el correspondiente autovalor de la matriz varianza-covarianza. Dado que λi2 nunca es negativo, para 
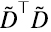los vectores singulares por derecha y por izquierda coinciden incluso en los signos, y son ortonormales entre sí como en (6.2-6.3).
Expresada la SVD de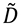 
en la forma (5.15), recordando que la traspuesta de un producto de matrices es el producto en orden inverso de las traspuestas y que (V⊤)⊤ = V, tenemos (6.11)
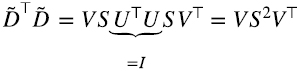
donde U⊤U es igual a la matriz identidad porque las columnas de U (filas de U⊤) son vectores ortonormales. Dado que la matriz S es diagonal con elementos λi, ver (5.16), la matriz S2 también es diagonal con elementos λi2. Es decir, obtenemos el mismo resultado que en (6.10) utilizando la forma (5.15) de SVD.
La expresión (6.11) de la matriz varianza-covarianza (proporcional a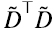 
) de la matriz de datos 
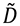se conoce como “análisis de componentes principales” (PCA) de 
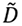. Como vemos, no es otra cosa que SVD aplicado a 
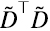, ver por ejemplo, Jolliffe y Cadima (2016).
Pero dado que los vectores singulares por derecha y por izquierda de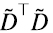 
son idénticos, además de la interpretación estadística que acabamos de ver, PCA tiene una interesante interpretación geométrica: recordando que por ser V ortogonal, V⊤V = V⊤V = I, multiplicando 
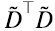en (6.11) por izquierda por V⊤ y por derecha por V obtenemos (6.12):
Siendo V ortogonal, se puede mostrar que V implementa en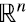 
una suerte de “rotación” (pueden también ser reflexiones, en general se llaman “transformaciones ortogonales”), y que el producto del lado derecho de la igualdad en (6.12) es exactamente cómo se “ve” la matriz 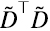en el sistema de coordenadas rotado por V, que transforma la base canónica en la base de autovectores de 
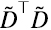. En ese sistema de coordenadas, dicha matriz es la matriz diagonal S2 en el lado izquierdo de la igualdad en (6.12).
Estadísticamente significa que la matriz V transforma las variables aleatorias muestreada en las columnas de D, que en general tienen covarianzas (6.8) (o correlaciones) no nulas entre sí, en variables aleatorias independientes (por lo menos hasta segundo orden).
Por supuesto podemos hacer el mismo tipo de aproximación de bajo rango de la matriz varianza-covarianza (6.10), o (6.11), simplemente reemplazando los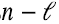 
valores singulares λi2 más pequeños por cero, obteniendo de esa manera la mejor aproximación de rango 
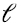de la matriz varianza-covarianza, ver (5.18-5.19). Vemos entonces que en el hecho de que esta aproximación tiene sentido, se basa la idea de análisis de factores, tan influyente en las ciencias humanas y sociales.
La “mejor aproximación de rango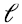 
“ de la matriz varianza-covarianza, que ya fue explicada en general en la sección 5, para esta matriz cuadrada, simétrica y semidefinida positiva, en la que, por lo tanto, el espacio fila y columna (ver sección 3) son en realidad el mismo espacio 
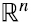donde viven los datos, implica dos nuevas interpretaciones complementarias y consistentes entre sí (recordemos que las filas de D son m puntos-dato que viven en 
.)
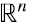Mirada desde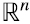 
que, de nuevo, es a la vez el espacio fila y columna de 
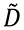, la mejor aproximación de rango 
es la mejor proyección de los 
puntos-dato dados por las filas de 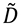en el “mejor” subespacio de 
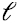dimensiones. Mejor en el doble sentido de ser el subespacio de 
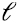dimensiones que captura la mayor varianza de los datos, explicando la mayor variabilidad de los mismos, y mejor en el sentido de ser el subespacio de 
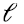dimensiones que minimiza la distancia al cuadrado de los puntos a dicho subespacio. Es decir, PCA es la mejor reducción dimensional lineal de los datos originales, y muchas veces conduce a una mejor interpretación de estos.
Mas allá de que por lo expresado en esta sección queda claro que se pueden calcular numéricamente los componentes principales de una matriz usando el software de SVD indicado en la introducción, hay software específico que puede resultar más conveniente, ver por ejemplo https://la.mathworks.com/help/stats/pca.html en Matlab, o https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html en la biblioteca scikit-learn de Python.
7. Ejemplo numérico
En esta sección se presenta un simple ejemplo numérico de lo visto en este artículo. El entorno es Jupyter Notebook de Anaconda.
Figura 3. Generación de datos y datos centrados
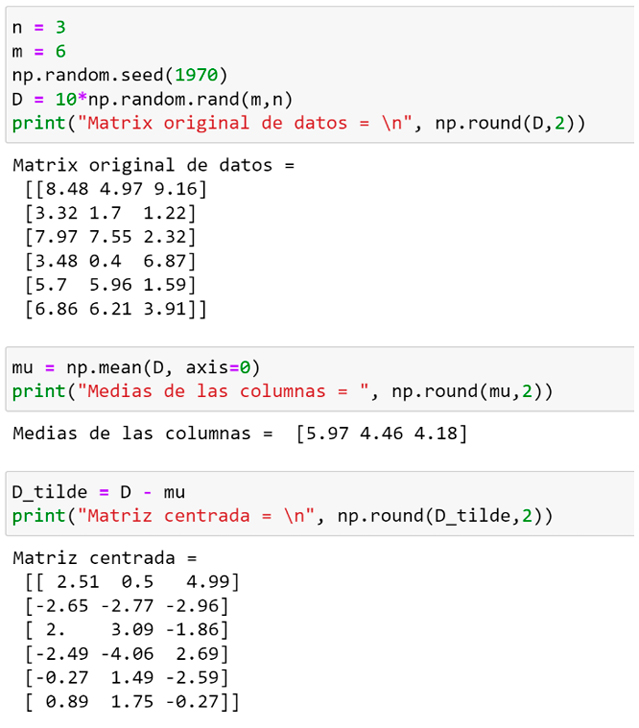
En la primera celda de la Figura 3 generamos una matriz 6x3 de datos. Cada elemento de la matriz D (“matriz original de datos”) es una muestra de una variable (pseudo)aleatoria que toma valores entre 0 y 10 con densidad de probabilidad constante. Se incorpora la “semilla” np.random.seed() por replicabilidad. En la segunda celda calculamos la media de cada columna (axis = 0). En la tercera celda se calcula la matriz centrada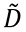 
: D_tilde = D – mu (se hace uso de Python broadcasting, ver https://numpy.org/doc/stable/user/basics.broadcasting.html). Se pudo haber calculado la SVD de la matriz D, pero se la centro primero para comparar luego con el cálculo PCA de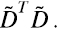 
Figura 4. Cálculo de la SVD de la matriz centrada con la función svd de la biblioteca linalg de numpy.
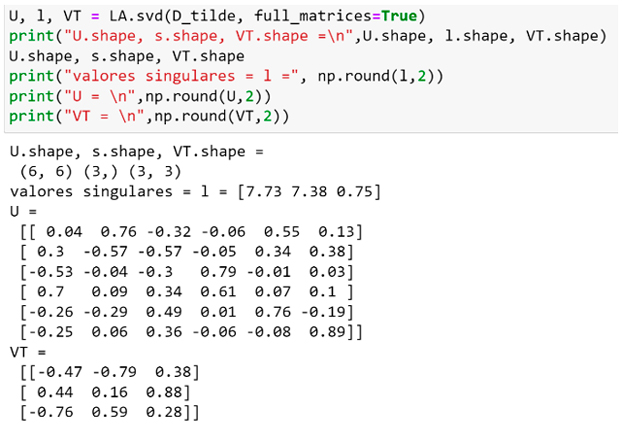
Notar en la Figura 4 que la función svd devuelve sólo los elementos diagonales λj (“l” en la figura) de la matriz diagonal Λ de la ecuación (1.9).
En la Figura 5 expresamos la matriz Λ en la forma en que aparece en (1.9). Notar que el tercer valor singular es en magnitud aproximadamente el 10% de los dos primeros.
Figura 5. En la segunda celda se observa la matriz Λ (L en la figura) tal como aparece en la ecuación (1.9). En la tercera celda se confirma que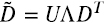 
(comparar con la matriz centrada de la figura 3).
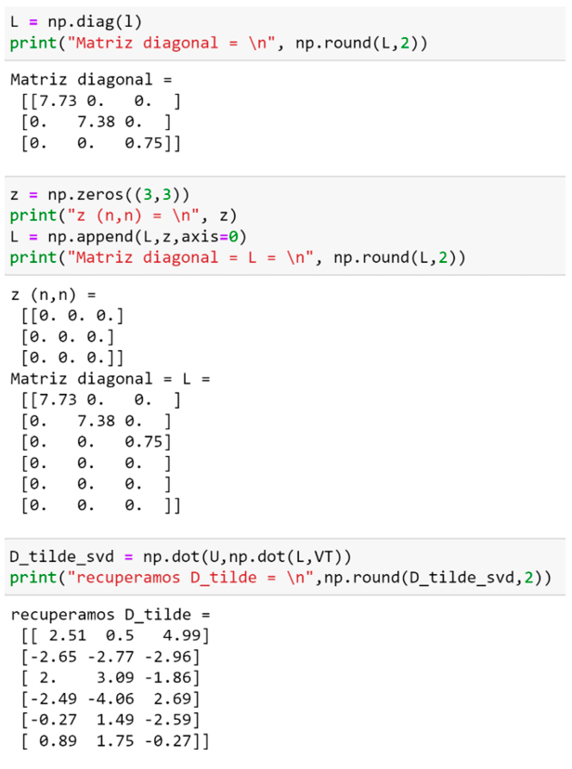
Figura 6. SVD de la matriz 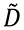con la función randomized_svd de la biblioteca scikit-learn.
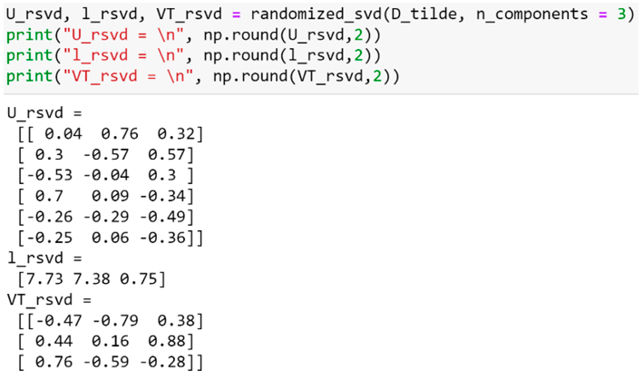
En la Figura 6 calculamos la SVD de la matriz con la función randomized_svd de la biblioteca scikit-learn, esta función es particularmente rápida para matrices grandes en las que desea extraer sólo una pequeña cantidad de valores singulares. Entrega solo 3 columnas de U, que son las que realmente se usan en SVD. Además, como se muestra en la Figura 7, es muy fácil truncar la cantidad de valores singulares que se desea.
Notar que la tercera columna de U_rsvd y la tercera fila de VT_rsvd tienen, signos opuestos a los de la tercera columna de U y la tercera fila de VT en la Figura 4. En el producto de la ecuación (1.9) para recuperar a la matriz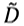 
con esa diferencia de signos se cancela.
Figura 7. SVD truncada (solo los primeros dos valores singulares, n_components = 2) de la matriz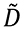 
con la función randomized_svd de la biblioteca scikit-learn.
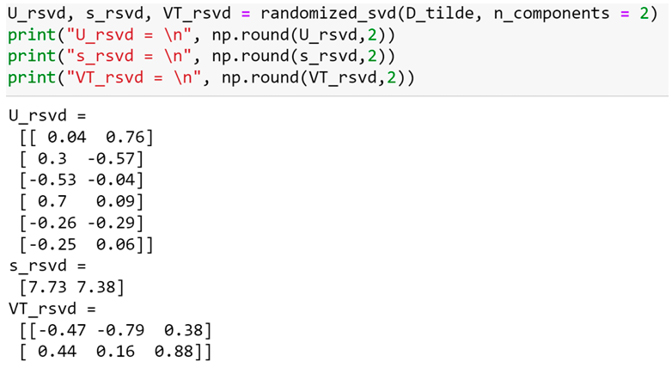
En la Figura 7 se observa que la SVD truncada de la matriz se obtiene simplemente igualando a cero los valores singulares que se desean truncar. En la figura 8 se ve la mejor aproximación de rango 2 de la matriz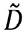 
.
Figura 8. D_tr denota a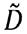 
con el tercer valor singular truncado.
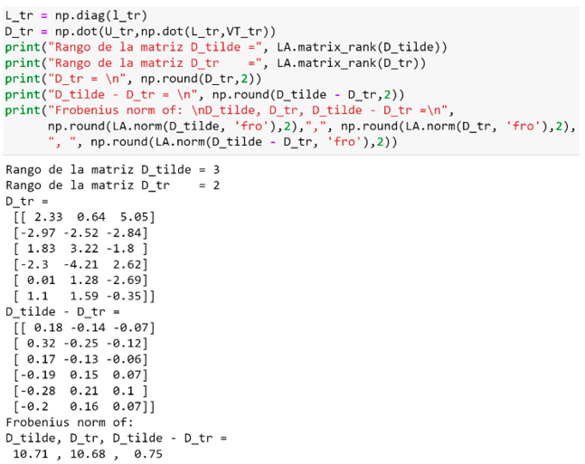
En la Figura 8 se calcula la matriz D_tr, que es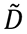 
manteniendo solo los primeros dos valores singulares, se comprueba que mientras que el rango de la matriz original es 3, el de la truncada es dos, y se comparan sus respectivas normas de Frobenius.
Figura 9. DTD denota a la matriz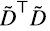 
de la matriz D de la figura 3.
En la primera celda de la figura 9 se obtiene a la matriz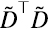 
(recprdar que 
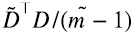es la estimación empírica de la matriz varianza-covarianza de los datos en D). En la segunda celda se comprueba que los autovalores de esta matriz (valores principales de su PCA) corresponden al cuadrado de los valores singulares de la matriz 
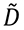, y sus autovectores son idénticos a los vectores singulares por derecha de 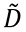. En la figura se imprime la traspuesta de VT para facilitar la comparación con los autovectores de 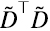. Distintos algoritmos pueden dar por respuesta autovectores que difieren entre si en un factor “-1” que preserva la normalización a 1.
Mientras que, por convención, al calcular la SVD los valores singulares se ordenan de mayor a menor, al calcular los autovalores, estos se ordenan en el orden opuesto y lo mismo ocurre para los correspondientes autovectores.
8. Conclusiones
En este trabajo nos planteamos dos objetivos. Ante el hecho de que en las ciencias humanas y sociales el análisis de factores es de gran importancia, el primer objetivo es presentar de manera accesible para cualquier persona en estas disciplinas con una base elemental de álgebra lineal, la técnica conocida como “descomposición en valores singulares”.
Dicha técnica sistematiza y generaliza el análisis de factores. Además, tiene implementaciones algorítmicas sumamente optimizadas, lo que la hace apta para el análisis de factores incluso en la era de “Big Data”, donde las bases de datos son mucho más voluminosas de lo que solían ser, tanto en número de puntos-dato como en la dimensión de estos.
Se eligió un camino para presentar la SVD que conduce a una comprensión intuitiva y a la vez rigurosa del método, así como su relación con PCA. Se presentaron varios ejemplos de dichas aplicaciones y se mostró su implementación práctica en Matlab y Python.
El segundo objetivo de este trabajo era hacer ciertas observaciones sobre el análisis de factores como idea fuerza de investigación en ciencias humanas y sociales en general. Las mismas requieren sólo unas pocas líneas con las que concluimos esta última sección.
Como se mencionó, la SVD sistematiza y generaliza el análisis de factores, pero también que le quita cierta mística. Bajo la lente de la SVD, no es sorprendente identificar una teoría de factores, ya que los factores son inherentes a cualquier conjunto de datos que pueda ser estructurado matricialmente. El verdadero valor o relevancia puede residir en la rapidez con la que los valores singulares disminuyen.
La SVD se puede pensar como el esqueleto formal de todas las posibles teorías de factores lineales. Esto es especialmente útil en la era de big data y machine learning. Si todo evoluciona como es de esperar, las ciencias humanas y sociales contarán pronto con bases de datos de escala y granularidad inimaginables pocos años atrás. SVD sin duda jugará un rol de creciente importancia en el análisis de estas.
¿Cómo se sostendrán las teorías de factores tradicionales, algunas de las cuales fueron mencionadas en la introducción, dada su dependencia en un número reducido de factores? Resulta difícil predecirlo. Pero puede ser útil reconocer de antemano que la supervivencia de estas descansa sobre la hipótesis implícita de que el número de valores singulares significativos se mantendrá relativamente pequeño, aun cuando las bases de datos aumenten en tamaño y dimensionalidad varios órdenes de magnitud. Serán los datos los que ofrezcan la respuesta definitiva.
8. Referencias
, , & (2000). Singular value decomposition for genome-wide expression data processing and modeling. Proceedings of the National Academy of Sciences of the United States of America, 97(18), 10101–10106.
, , , , & (2021). Matrix completion methods for causal panel data models. Journal of the American Statistical Association, 116(536), 1716-1730.
(2019). 21. The Impact of Machine Learning on Economics. In A. Agrawal, J. Gans & A. Goldfarb (Ed.), The Economics of Artificial Intelligence: An Agenda (pp. 507-552). Chicago: University of Chicago Press.
, & (2019). Machine learning methods that economists should know about. Annual Review of Economics, 11, 685-725.
, & (2002). Determining the number of factors in approximate factor models. Econometrica, 70(1), 191-221.
, & (2008). Large dimensional factor analysis. Foundations and Trends® in Econometrics, 3(2), 89-163.
, , , , & (2016). Man is to computer programmer as woman is to homemaker? Debiasing word embeddings. Advances in Neural Information Processing Systems, 29: https://scholar.google.com/scholar_lookup?arxiv_id=1607.06520
(1909). Experimental tests of general intelligence. British Journal of Psychology, 3(1), 94.
, , , , & (1990). Indexing by latent semantic analysis. Journal of the American Society for Information Science, 41(6), 391-407.
, & (1936). The approximation of one matrix by another of lower rank. Psychometrika, 1(3), 211-218.
(1919). On certain independent factors in mental measurements. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 96(675), 91-111.
(1976). Modern factor analysis. University of Chicago press.
, , , , , & (2000). Fundamental patterns underlying gene expression profiles: simplicity from complexity. Proceedings of the National Academy of Sciences, 97(15), 8409-8414.
(1930). Statistical résumé of the Spearman two-factor theory. (Mimeographed).
, & (2016). Principal component analysis: a review and recent developments. Philosophical transactions of the royal society A: Mathematical, Physical and Engineering Sciences, 374(2065), 20150202.
(2007). Álgebra Lineal y sus Aplicaciones. Pearson educación.
, , , , & (2007). Randomized algorithms for the low-rank approximation of matrices. Proceedings of the National Academy of Sciences, 104(51), 20167-20172.
(1975). The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets. In Stochastic optimization models in finance (pp. 131-155). Academic Press.
(1966). Equilibrium in a capital asset market. Econometrica: Journal of the Econometric Society, 768-783.
, , & (2004). Singular value decomposition, eigenfaces, and 3D reconstructions. SIAM Review, 46(3), 518-545.
, , , , , , ... & (2008). Genes mirror geography within Europe. Nature, 456(7218), 98-101.
(1901). LIII. On lines and planes of closest fit to systems of points in space. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 2(11), 559-572.
(2013). The arbitrage theory of capital asset pricing. In Handbook of the fundamentals of financial decision making: Part I (pp. 11-30).
(1964). Capital asset prices: A theory of market equilibrium under conditions of risk. The Journal of Finance, 19(3), 425-442.
(1904). General Intelligence, Objectively Determined and Measured. The American Journal of Psychology, 15(2), 201-292. https://doi.org/10.2307/1412107.
(1927). The Abilities of Man: Their Nature and Measurement. Journal of Philosophical Studies, 2(8), 557-560.
(1993): On the Early History of the Singular Value Decomposition. SIAM Review, 35(4), 551-566.
& (2011). Dynamic factor models. Oxford Handbooks Online.
&(2015). Factor Models for Macroeconomics. En Taylor, J. B. y Uhlig, H. (Eds.), Handbook of Macroeconomics (Vol. 2). North Holland.
(1938). Methods of Estimating Mental Factors. Nature, 141, 246.
(1931). Multiple factor analysis. Psychological Review, 38(5), p. 406.
(1947). Multiple-factor analysis; a development and expansion of The Vectors of Mind. University of Chicago Press.
, & (1991a). Eigenfaces for recognition. Journal of cognitive neuroscience, 3(1), 71-86. https://scholar.google.com.ar/scholar?q=Eigenfaces+for+recognition.+Journal+of+Cognitive+Neuroscience,+(3).&hl=es&as_sdt=0&as_vis=1&oi=scholart
& (1991b). Face recognition using Eigenfaces. Proc. of Computer Vision and Pattern Recognition, (3), 586-591.