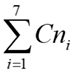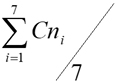Procedimiento para la selección de proyectos turísticos, una aplicación de preferencia borrosa. Caso Destino Playa Santa Lucia, Cuba
Procedure for the selection of tourism projects, a fuzzy preference application. Case Destination Playa Santa Lucia, Cuba
Jesús M. Rodríguez Rubinos
Universidad de Camagüey Ignacio Agramonte Loynaz (Cuba)
https://orcid.org/0009-0000-8983-5730
Yaquelín Arzuaga Camacho
Universidad de Camagüey Ignacio Agramonte Loynaz (Cuba)
https://orcid.org/0009-0007-1158-9665
yaquelin.arzuaga@reduc.edu.edu
Claudia A. Alonso Toirán
Universidad de Camagüey Ignacio Agramonte Loynaz (Cuba)
https://orcid.org/0009-0001-8275-5970
Miguel Ramírez Reyes
Universidad de Camagüey Ignacio Agramonte Loynaz (Cuba)
https://orcid.org/0000-0002-8832-1532
RESUMEN
Se propone un procedimiento para la selección de proyectos turísticos en Camagüey, en un ambiente de restricciones, mediante la preferencia borrosa. Para el desarrollo de la investigación se emplearon como métodos empíricos, la revisión bibliográfica y documental de información, tanto primaria como secundaria, entrevista a especialistas, expertos y directivos del Ministerio de Turismo en Camagüey, los métodos estadísticos, modelos matemáticos de preferencia borrosa y la aplicación del método de opinión de expertos. Se obtuvo un procedimiento estructurado en etapas donde se determinó a través de un modelo de preferencia borrosa, el ordenamiento por prioridades, en medio de incertidumbres, de la cartera de proyectos del MINTUR. El procedimiento de la identificación de indicadores y las herramientas para la toma de decisiones, mediante la ordenación comparada de mejor a peor de los proyectos turísticos en Camagüey, en una aplicación de las relaciones de preferencia borrosas, es pertinente y adecuado a la selección de proyectos turísticos atendiendo a las necesidades de priorizar los proyectos que impacten en el desarrollo dentro de las restricciones de recursos. Se cumple el objetivo de una propuesta adecuada a las condiciones de incertidumbre, ofreciendo un enfoque integral de la selección no reducida a indicadores económicos financieros. En un ejercicio de validación sobre tres proyectos de disímiles naturaleza e impacto sobre el turismo en el destino Playa Santa Lucía, seleccionan el proyecto de nuevo producto náutico sobre los proyectos hoteleros y dentro de los hoteleros, la renovación radical frente a nueva instalación.
PALABRAS CLAVE
Ordenación comparada; preferencia borrosa; selección de proyectos; turismo.
ABSTRACT
Is propose a procedure for the selection of tourist projects in Camagüey, in an environment of restrictions, through the blurred preference. For the development of research, were used as the empirical methods, the bibliographic and documentary review of information, both primary and secondary, interview with specialists, experts and directors of the Ministry of Tourism in Camagüey, statistical methods, mathematical models of blurred preference and the application of the method of expert opinion. A structured procedure was obtained in stages where it was determined through a model of blurred preference, the ordering by priorities, in the midst of uncertainties, of the MINTUR project portfolio. The procedure of the identification of indicators and tools for decision-making, through the comparative management from best to worst of tourism projects in Camagüey, in an application of blurred preference relationships, is relevant and appropriate to the selection of tourism projects according to the needs of prioritizing projects that impact development within resource constraints. The objective of a proposal appropriate to the conditions of uncertainty is met, offering a comprehensive approach to selection not reduced to financial economic indicators. In a validation exercise on three projects of dissimilar nature and impact on tourism in the Playa Santa Lucía destination, they select the new nautical product project on hotel projects and within hoteliers, the radical renovation in the face of a new facility.
KEYWORDS
Comparative planning; fuzzy preference; project selection; tourism.
Clasificación JEL: C65; O22.
MSC2010: 90B99.
1. Introducción
El turismo en Cuba representa el 10 % al Producto Interno Bruto (PIB) y genera más de medio millón de empleos (Salinas, Salinas y Mundeti, 2019). Tuvo un crecimiento promedio anual del 11 % entre 1990 y 2007 y del seis por ciento hasta el 2016. Alcanzó en el año 2018 los 4,711,910 visitantes internacionales y un ingreso de 2,782.2 millones de pesos convertibles asociados al turismo internacional (Oficina Nacional de Estadística e Información [ONEI], 2021).
A partir del segundo semestre del año 2019, las visitas turísticas a Cuba decrecieron, afectados por la pandemia COVID-19 y a medidas restrictivas del gobierno de los Estados Unidos que limitaron el flujo turístico del mercado norteamericano (Mesa Redonda, 9 de septiembre de 2021).
Al cierre del 2019 se reportaron 4,275,558 visitantes internacionales, lo que significó un nueve por ciento menos que en el año anterior (ONEI, 2021). Con la llegada de la pandemia del COVID-19 a Cuba, el 2020 cerró con solo 1,085,920 de visitas internacionales, mientras que el 2021 lo hizo con unos 573,944 viajeros, un 39.8 por ciento de quienes visitaron el país en el año anterior y equivale a 869,181 turistas menos (Cubadebate, 6 de febrero de 2022).
La etapa Post-COVID se caracteriza por nuevas tendencias en el turismo (Ostelea, 2021) como los viajes nacionales o domésticos, el turismo familiar, el disfrute de espacios abiertos mediante la práctica del turismo rural, el comunitario como alternativa al urbano convencional y el turismo de naturaleza que ha sentado las bases para el desarrollo de otros tipos de turismo como el agroturismo, ecoturismo, turismo salvaje y de aventura (Rivero, Portela y Cabrera 2022). Las actuales tendencias, han demostrado que no solo se necesitaba la renovación de algunos productos, sino la reinserción de nuevos proyectos en el vigente contexto.
En este escenario, el producto turístico camagüeyano mantiene el comportamiento de una marcada tendencia al estancamiento-declive identificado en estudios previos a la pandemia, según Rodríguez (Ed.) (2012), necesitado de la renovación e incremento de sus ofertas y servicios para su inserción competitiva en el escenario turístico actual. El Ministerio de Turismo (MINTUR) en el territorio y su sistema empresarial poseen un grupo de propuestas de proyectos para la introducción de nuevos productos turísticos y mejoras radicales a los existentes, que requieren de importantes inversiones que impacten en dinamizar el sector y abordar nuevos mercados y canales de distribución de una manera más integral.
Se han desarrollado herramientas de ordenamiento de mejor a peor de proyectos para la toma de decisiones, creadas fundamentalmente en ambientes de certidumbre y que involucran el problema de selección de un conjunto de propuestas con respecto al cumplimiento de indicadores ordenados, como el método de jerarquía analítica de Saaty (Bravo, Schulz, Romero, López y Güereca, 2021) y Electre (Fernández y Olmedo, 2007) que constituyen antecedentes teóricos de la investigación. Más reciente se han aplicado nuevas herramientas para ejecutar estos procesos a través de la lógica borrosa (Romero, Meléndez y Andino, 2020), adecuada a ambientes de incertidumbre y se emplea para reproducir las formas en las cuales las personas y los expertos piensan y toman decisiones (Juca, García y Carrión, 2020).
El proceso de toma de decisiones, sobre qué proyectos priorizar, en un ambiente de fuertes restricciones y limitantes materiales y financieras, demanda de un procedimiento que permita seleccionar de la cartera de proyectos del MINTUR, aquellos que tengan un mayor impacto sobre la recuperación del destino turístico.
Este trabajo se enfoca en proponer un procedimiento para la selección de proyectos turísticos en Camagüey, en un ambiente de incertidumbre, mediante la preferencia borrosa.
Se utilizaron como métodos teóricos, el histórico-lógico para reflejar la conexión histórica fundamental que se observa entre los conceptos y reportes de investigaciones a lo largo del tiempo y las regularidades encontradas, y el análisis y síntesis para determinar cuáles indicadores son más efectivos. Se emplearon técnicas cuantitativas al aplicar modelos matemáticos de preferencia borrosa y la aplicación del método de opinión de expertos o Delphi para las opiniones subjetivas, el grado de acuerdo, desacuerdo o indecisión.
Como resultado se propone un procedimiento estructurado en etapas, que, a través de un modelo matemático sustentado en la preferencia borrosa, facilita el ordenamiento por prioridades, en medio de incertidumbres, de la cartera de proyectos del MINTUR.
2. La cartera de proyectos turísticos, herramientas para su selección.
La conceptualización de proyecto, según Rentería (2018), nos acerca a un conjunto de actividades interrelacionadas para transformar recursos y suministrar bienes y servicios, bajo una unidad de dirección, hacia un objetivo determinado, en un tiempo definido.
La norma internacional Sistemas de calidad en la gestión de proyectos con ISO 10006, ISO (2017), lo conceptualiza como: “proceso único que consiste en un conjunto de actividades coordinadas y controladas, con fechas de inicio y terminación, destinadas a lograr un objetivo en conformidad con requisitos específicos, incluyendo las limitaciones impuestas por el tiempo, el costo y los recursos.”
Medinilla y Velasteguí (2018), plantean que puede ser definido como cualquier actividad con un momento de referencia de inicio y con metas u objetivos precisos que determinan su conclusión. Por otra parte, Solís (2009) destaca el conjunto relacionado y afín de actividades encauzadas hacia uno o varios objetivos a través una metodología determinada, para lo cual es necesario de un equipo de trabajo idóneo, además de, recursos materiales y financieros expresado en un presupuesto, para el logro de resultados esperados siguiendo normas y prácticas comúnmente aceptadas, con una programación en el tiempo que garantice una duración limitada.
A su vez, Heredia (1995), lo ha definido como “la combinación de recursos humanos y no humanos reunidos en una organización temporal con el fin de lograr un propósito determinado”. Para PMBOK (2017), un proyecto es un esfuerzo que se lleva a cabo para crear un producto, servicio o resultado único, y tiene la característica de la temporalidad, por tanto, con inicio y final dado, y este se logra cuando se alcanzan los objetivos y metas del proyecto o cuando se abandona o cierra porque no es, ni será posible cumplirlos, o desaparece la necesidad que dio origen al proyecto.
Los autores coinciden en que un proyecto es un conjunto de esfuerzos o actividades que se realizan con un objetivo específico, enmarcado en un tiempo limitado de inicio y terminación. Requiere de recursos y es necesario contar con las personas idóneas que controlen la ejecución del proyecto.
La selección de proyectos es el proceso encargado de generar la lista de proyectos a ejecutar, a partir de la evaluación y la comparación entre criterios de selección por cada uno de estos, es una decisión estratégica, ante la limitación de recursos y la responsabilidad de generar beneficios (Rentería, 2018). Este autor advierte acerca de las consecuencias negativas de los errores en la selección de los proyectos que conforman un portafolio, con un enfoque desbalanceado, falta de integración y coherencia con las metas estratégicas de la organización.
Vidal (2012), plantea la necesidad de evaluar varias propuestas atendiendo a criterios para realizar la selección y tomar decisión por la mejor opción para convertirla en el proyecto que beneficiará a la organización en mayor medida. Destaca su complejidad, debido a que se tiene que elegir la mejor alternativa para que la empresa decida invertir los recursos, alcanzar sus objetivos y optimizar resultados. Decantarse por un proyecto o un portafolio de proyectos es vital para resolver el problema de distribuir los escasos recursos de una organización entre el conjunto de alternativas o proyectos candidatos a financiar e implementar (Vidal 2012).
Por tanto, la selección de los proyectos dentro de una cartera o portafolio, requiere de comparar la pertinencia de estos referidos a un conjunto de atributos, para determinar los de mejor mérito. Conviene destacar la complejidad del proceso en cuanto a la selección de los atributos de la decisión y de su complementación.
Se han desarrollado y aplicado diversos modelos, métodos o metodologías para la evaluación de proyectos. Los métodos económicos más comunes, (Fernández, Gómez, Guerrero y Caballero (2008), Aponte, Muñoz y Álzate, (2017)), son: Valor Actual Neto (VAN), Tasa Interna de Rentabilidad (TIR), Periodo Mínimo de Recuperación de la Inversión y Ratio Beneficio-Coste. Estos indicadores económicos financieros sustentan la decisión de aprobación de la viabilidad del proyecto según MEP (2014).
Los métodos de ordenación (ranking), permiten determinar una jerarquía u orden de preferencia de los proyectos candidatos, que cumplen los requisitos de viabilidad financiera, basándose en un conjunto de criterios, que supera el enfoque financiero y permite englobar en la decisión otros factores, como sociales, ambientales, legales, para que el agente decisor, en función de los recursos disponibles, seleccione los proyectos en orden, hasta agotar los recursos. Para crear un ranking entre proyectos, se valora cada proyecto o alternativa en función de atributos o criterios a tener en cuenta en el proceso de toma de decisiones. Los modelos más usuales son: métodos comparativos y scoring. En los métodos comparativos, cada proyecto se compara con otro proyecto o grupo de proyectos alternativos. Dentro de estos modelos, los más utilizados son: conteo de la dominancia y el método de escala anclada para establecer un orden entre los proyectos (Fernández, Gómez, Guerrero y Caballero, 2008).
Los Modelos de scoring, se basan en una expresión algebraica que produce una puntuación para cada proyecto en consideración, teniendo en cuenta los n factores o criterios considerados más importantes por parte de los decisores. Para obtener esa valoración, cada uno de estos criterios es ponderado en relación a su importancia relativa con respecto al resto de criterios. Dentro de los modelos de scoring, según Fernández, Gómez, Guerrero y Caballero (2008) se encuentran: checklist, scoring tradicional y análisis de utilidad multiatributo (MAUT).
Una de las herramientas aplicadas a la selección de proyectos es el método Analytic Hierarchy Process (AHP), propuesto por Thomas Saaty en 1980, según Saaty-Vargas (2001), un método cuantitativo multicriterio para la toma de decisiones, que permite dar prioridades o jerarquías apoyándose en el juicio de expertos a través de comparaciones por pares, basándose en una escala de preferencia entre dos alternativas. Esta escala permite incorporar un modelo de decisión, representando la preferencia de una alternativa frente a otra en relación con un atributo (Nantes, 2019).
Según Nantes (2019), para Saaty el proceso de decisión con AHP abarca la definición del problema, la estructuración del problema a través de la descomposición jerárquica en atributos y subatributos, la construcción de matrices de comparación de los juicios de expertos y, por último, la síntesis de cada una de las matrices en el modelo de la prioridad global de cada alternativa.
Otras herramientas desarrolladas para la toma de decisiones aplicadas a la selección de proyectos es el método ELECTRE, propuesto por el profesor Bernard Roy (Gaviño 2021), basado en relaciones de superación o sobre clasificación, para decidir acerca de la determinación de una solución, considerada satisfactoria, aunque no óptima, y obtener una jerarquización de las alternativas bajo estudio. Se han desarrollado múltiples procedimientos y sus variantes (ELECTRE I, II, III, IV, IS; y ELECTRE TRI), para solucionar disímiles problemas relacionados con la toma de decisiones (Reyes, Souto y Rodríguez 2019).
Emrouznejad y Ho (2017), apuntan que las aplicaciones de métodos multicriterios para la toma de decisiones (MCDM) utilizan datos nítidos, pero es posible también emplearlos en ambientes de incertidumbres e imprecisos. Se han desarrollado aplicaciones, AHP difuso (FAHP), para tratar con datos inciertos en la evaluación de la importancia relativa de los atributos y las comparaciones de las alternativas con respecto a los atributos.
Según Ortega, Erazo y Narváez, (2019), la Lógica Borrosa desarrollada por el investigador Lotfy Zadeh en la Universidad de Berkeley en California, analiza el principio de incompatibilidad, que estipula que mientras más complejo es un sistema, la capacidad de ser precisos disminuye, es así que construye una nueva teoría de conjunto difuso o Fuzzy Set (Fuller y Carlsson 1996) que toma en cuenta que el pensamiento humano no son números sino etiquetas lingüísticas, en el cual se representa el conocimiento común expresado cualitativamente.
Rivadeneira (2018) analiza la lógica borrosa como un conjunto de principios matemáticos basados en grados de membresía o pertenencia 𝝁𝑨(𝒙) del elemento 𝒙 en el conjunto difuso A, que puede variar de cero a uno, lo que permite modelar un problema en base a reglas lingüísticas. Esta lógica, a diferencia de la lógica convencional de valor discreto cero o uno, se presenta en rangos de membresía a un conjunto, en un valor entre cero y uno. Destaca además que en el campo de la toma de decisiones generalmente no es posible definir los hechos como totalmente verdaderos o falsos, sino, en términos de grado de verdad o falsedad. La lógica binaria (cierto o falso) no es la más adecuada para tratar este tipo de razonamientos de decisión, porque excluye por completo una tercera posibilidad (o más) entre estos dos valores, (Nieto y Aragonés, 2015).
La selección de proyectos, como problema de toma de decisión, se corresponde con una realidad de imprecisión e incertidumbre. La preparación de una decisión obedece más a criterios vagos que a criterios precisos, por lo que la toma de decisiones, en ambientes de incertidumbre, complejos, no debe estudiarse en términos de exactitud, con técnicas ajustables a escenarios ciertos, pues en la búsqueda de la precisión intentando ajustar el mundo real a modelos matemáticos rígidos, se pierde información valiosa, (Entenza, Argüelles y Dorta (2018), Rivadeneira (2018), Juca, García y Carrión (2020))
En este sentido, la capacidad de representar el pensamiento humano hace que la lógica borrosa sea una metodología ideal para el desarrollo de modelos y sistemas basados en el conocimiento, y criterios de expertos, que son de mucha ayuda para herramientas de apoyo para la toma de decisiones, como es el caso de la selección de proyectos en ambientes de incertidumbre y restricción de recursos.
3. Procedimiento para la selección de proyectos en ambientes de incertidumbre
Los procesos de selección de proyectos turísticos, dentro de un conjunto de alternativas, se enfrenta al problema de definir los atributos sobre los cuales se establecerán las comparaciones, dado la especificidad y contexto en el cual se realiza. La participación de expertos requiere de adecuada selección y empleo de técnicas para reducir la subjetividad de todo proceso de selección (Reyes, Souto y Rodríguez, 2019).
El procedimiento propuesto está sustentado en las Relaciones de Preferencia Borrosa desarrollada en Orlovskii (1980), que le brinda una mayor flexibilidad y la posibilidad de atenuar la subjetividad presente en la toma de decisiones en ambiente de incertidumbre.
Para realizar el procedimiento con respecto a la selección de proyectos turísticos en Camagüey, y obtener los resultados propuestos, se propone:
1.Caracterización de la cartera de proyectos turísticos del territorio.
Objetivo: Caracterizar la cartera de proyectos turísticos del territorio.
Contenido: Proyectos del Plan de Desarrollo del Polo Turístico Santa Lucía y Nuevitas y del Plan de Desarrollo Camagüey. Monto de inversión. OSDE operador. Programa al que pertenece. Tipo de instalación. Estado de la preparación de la inversión. Indicadores técnicos, comerciales y financieros.
Descripción: Entrevista no estructurada y estudio de la documentación, informes y reportes de los planes de desarrollo del turismo en Camagüey, que están avalados por los organismos del sector. Se podrá trabajar con nuevos productos turísticos y las mejoras a los existentes para el logro de una mayor dinamización del sector. Análisis y procesamiento de la información de cada proyecto a través de las tablas y fichas de contenido para su entendimiento.
A cada proyecto turístico de la cartera obtenida, se le realizará una ficha resumen de proyecto, donde se precisen los datos más significativos para la identificación y el conocimiento de su desarrollo, monto de inversión, estado de la inversión, resultados de la evaluación y del Estudio de Oportunidad, Prefactibilidad o Factibilidad, según proceda.
2.Identificación de indicadores principales de evaluación para la selección de proyectos.
Objetivo: Identificar los indicadores que permitan la comparación para la selección de proyectos.
Contenido: Indicadores económicos, financieros, comerciales, ambientales, de gestión, y técnicos.
Descripción: Revisión bibliográfica y entrevistas a implicados en la gestión de proyectos para conformar propuesta de indicadores. Consulta a grupo de expertos para la validación de los indicadores principales de evaluación para la selección de proyectos. Selección de expertos según Coeficiente de Competencia de los expertos (K), el cual se obtiene a partir de dos componentes: Coeficiente de Conocimiento (Kc) y Coeficiente de Argumentación (Ka) (Reyes, Souto y Rodríguez, 2019).
Consulta por rondas mediante encuesta, en una escala del 1 al 5, sobre la pertinencia de los indicadores para la selección de proyectos turísticos hasta lograr concordancia mayor del 65 % (Cuesta 2001).
3.Aplicación de la herramienta de preferencia borrosa de alternativas frente a un criterio de decisión para la selección de proyectos.
Objetivo: Aplicar la herramienta de preferencia borrosa de alternativas frente al conjunto de criterios de decisión para la selección de proyectos, con la participación de expertos, (Cabrero y Llorente 2013). El procedimiento se sustenta en la propuesta de Orlovskii (1981), una aplicación de la lógica difusa de preferencia, implementada en Rodríguez, Betancourt y Escobar (2006).
Descripción: Selección del grupo de expertos para el apoyo a la evaluación multicriterio,. Socialización entre los expertos de las fichas de proyectos y de los indicadores seleccionados. Definición por los expertos del grado de importancia de cada criterio en el conjunto, método de Jerarquía Analítica Difuso, (Emrouznejad y Ho, 2017). Valoración de las relaciones de preferencia difusa entre los proyectos objeto del estudio comparado, según cada criterio de evaluación.
Aplicación y determinación de la preferencia y alternativa no dominada al máximo. Valoración cualitativa de los resultados apoyada en el método multicriterio para la toma de decisiones, sustentada en las relaciones difusas de preferencias.
4. Relaciones de preferencia borrosa para la selección de proyectos turísticos.
La identificación de las alternativas de decisión de proyectos a priorizar dentro del Programa de desarrollo del turismo al 2030 se realizó teniendo en cuenta la cartera de proyectos turísticos que gestiona la Delegación del MINTUR en Camagüey, que se corresponde con el Programa de Desarrollo al 2030. Se identificaron 26 proyectos en diferentes fases de preparación. Los proyectos de alojamientos tienen el mayor peso dentro del conjunto, con un total de 19 (73 %), lo que refuerza el criterio de una estrategia de desarrollo basada en hoteles en detrimento del producto náutico-recreativo y de la integralidad de la experiencia turística.
El programa de alojamientos abarca 2107 habitaciones. De ellas, 448 habitaciones corresponden a seis nuevos hoteles, uno de 300 habitaciones en el destino Playa Santa Lucía, dos hoteles con 29 habitaciones en la modalidad de turismo rural y tres Hoteles E con un total de 91 habitaciones con un producto urbano cultural. Se ampliarán seis hoteles con 195 nuevas capacidades.
Se proyecta la mejora del producto de cinco hoteles en 1193 habitaciones y se prevé intervenir en tres hoteles y sus 271 habitaciones, en un cambio de marca y de nuevos estándares, según Meliá Hoteles Internacional. Este programa de alojamientos demanda un financiamiento estimado de 588,027.0 MP.
El programa náutico contempla tres nuevos productos, Base náutica con 100 atraques, Funicular acuático y Parque acuático y, la mejora del producto Playa Bonita, con nuevas capacidades recreativas, gastronómicas y náuticas. Referente al Programa de recreación solo se incluye el nuevo producto Ocio Club Palmas del Mar.
Teniendo en cuenta el grado de avance de la preparación de los proyectos, no todos cuentan con los estudios de viabilidad técnica, comercial, económica y financiera a nivel de oportunidad, prefactibilidad o factibilidad, lo que constituye una limitación metodológica, a la vez que confirma el ambiente de ambigüedad e incertidumbre en el que se realiza el proceso de toma de decisiones.
Para validar el procedimiento propuesto se ha tomado como conjunto de alternativas, solo tres proyectos, representativos de la estrategia de desarrollo, en cuanto a proyectos propuestos de Nuevo Producto Náutico (NPN), Nuevo Producto Hotelero (NPH) y Mejoras de Producto Hotelero (MPH) y en cuanto a la complejidad de la toma de decisiones referente al crecimiento de habitaciones frente a la diversificación del producto.
Se define un conjunto de alternativas:
X = {x1, x2, x3}
Donde; X, es el conjunto de alternativas,
x1-Hotel Tararaco, Ampliación y mejora (MPH)
x2.- Hotel Residencial Santa Lucía (NPH)
x3- Base Náutica La Boca con 100 Atraques (NPN),
5. Selección de expertos, determinación de atributos y subatributos para la decisión y sus pesos relativos.
La determinación de los atributos y subatributos sobre los cuales se realizan las relaciones comparadas difusas para la toma de decisiones de selección de los proyectos, requirió de conformar un grupo de expertos, no solo seleccionados por su experticia sino también caracterizados por su involucración y compromiso con el objetivo de la investigación. Se trabajó con siete expertos, dos vinculados a la docencia e investigación universitaria, dos directivos del sector turístico con experiencia en la gestión de proyectos de inversión y tres especialistas en desarrollo turístico.
La evaluación de experticia arrojó un coeficiente de competencia de 0.85, resultados de un coeficiente de conocimientos de 0.81 y de argumentación de 0.90, con una desviación estándar de 0.051 en un intervalo de valor Max de 0.93 y Min de 0.78. Por ello, se valora que para K ≥ 0.8, el grupo de expertos seleccionados tiene un Coeficiente de Competencia alto.
A partir de la revisión documental, estudio de investigaciones precedentes, León, García y Guerra (2018), MEP (2014), Reyes, Souto y Rodríguez (2019), y de entrevistas realizadas a directivos del sector turístico se conformó la siguiente propuesta de atributos y subatributos a validar por los expertos.
C1- Económico; Costo de operación, Generación de ingresos, Impacto en la economía local, Encadenamiento productivo
C2- Social; Generación de empleos, Implicación socio-comunitaria
C3- Ambiental; Carga turística, Generación de desechos, Consumo energético, Uso de fuentes renovables, Contaminación Sonora, Emisión de gases, Uso del reciclaje, Sostenibilidad
C4- Técnica; Uso de nuevas tecnologías o informatización, Aprovechamiento de capacidades, Requerimiento tecnológico, Requerimientos de insumos y dotaciones iniciales
C5- Gestión; Prioridad en la política de Desarrollo, Ordenación del espacio, Criterios legales
C6- Financiera; VAN, TIR, Monto de Inversión, Fuente de Financiamiento, Período de recuperación
C7- Comercial; Mercado objetivo; Dinámica de la demanda; Competidores en la región
Teniendo en cuenta la propuesta de Cuesta (2001), se aplicó Delphi y en tres rondas se logró concordancia con coeficiente de Kendall de 0.63, aceptado (Si w>=0.5- Hay concordancia en el criterio de los expertos).
Debido a que en la definición de criterios múltiples no necesariamente todos tienen igual importancia y peso, resulta conveniente “ponderar” las decisiones a partir de asignar a cada uno de ellos un valor de “importancia relativa” dentro de la totalidad.
Según procedimiento basado en Saaty, de Fuller y Carlsson (1996), las comparaciones por pares, a partir de la matriz simétrica de comparación de cada elemento con el resto, resulta el conjunto:
Wp = {w1, w2, w3, w4, w5, w6, w7},
Donde: Wp son los pesos relativos de cada criterio, con la condición de 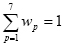
La matriz de comparaciones apareadas es cuadrada y reflexiva. Comparando por filas de izquierda a derecha cada elemento de la fila con cada uno de los elementos de las columnas, se cuestiona: ¿Cuán importante es el elemento Ci de la fila, respecto a los elementos Cj de las columnas?, según escala de Saaty, obteniendo así una matriz reflexiva, o sea, de diagonal principal unitaria dado que cada criterio respecto así mismo será de igual importancia:
|
Wp |
C1 |
C2 |
C3 |
C4 |
C5 |
C6 |
C7 |
|
C1 |
1.00 |
3.00 |
4.00 |
5.00 |
8.00 |
1.00 |
1.00 |
|
C2 |
0.33 |
1.00 |
3.00 |
4.00 |
8.00 |
0.33 |
0.33 |
|
C3 |
0.25 |
0.33 |
1.00 |
3.00 |
5.00 |
0.25 |
0.25 |
|
C4 |
0.20 |
0.25 |
0.33 |
1.00 |
2.00 |
0.20 |
0.20 |
|
C5 |
0.13 |
0.13 |
0.20 |
0.50 |
1.00 |
0.14 |
0.14 |
|
C6 |
1.00 |
3.00 |
4.00 |
5.00 |
7.00 |
1.00 |
1.00 |
|
C7 |
1.00 |
3.00 |
4.00 |
5.00 |
7.00 |
1.00 |
1.00 |
|
Σ |
3.91 |
10.71 |
16.53 |
23.50 |
38.29 |
3.92 |
3.92 |
Dividiendo cada celda entre el valor total de la columna correspondiente, obtenemos la matriz de pesos ponderados normalizados Cn, n=1,…,7, y calculando el valor medio por cada fila, obtenemos, para cada criterio su peso relativo dentro del conjunto, tal como se muestra:
|
Wp |
cn1 |
cn2 |
cn3 |
cn4 |
cn5 |
cn6 |
cn7 |
|
|
|
C1 |
0.256 |
0.280 |
0.242 |
0.213 |
0.209 |
0.255 |
0.255 |
1.709 |
0.244 |
|
C2 |
0.085 |
0.093 |
0.181 |
0.170 |
0.209 |
0.085 |
0.085 |
0.909 |
0.130 |
|
C3 |
0.064 |
0.031 |
0.060 |
0.128 |
0.131 |
0.064 |
0.064 |
0.541 |
0.077 |
|
C4 |
0.051 |
0.023 |
0.020 |
0.043 |
0.052 |
0.051 |
0.051 |
0.291 |
0.042 |
|
C5 |
0.032 |
0.012 |
0.012 |
0.021 |
0.026 |
0.036 |
0.036 |
0.175 |
0.025 |
|
C6 |
0.256 |
0.280 |
0.242 |
0.213 |
0.187 |
0.255 |
0.255 |
1.687 |
0.241 |
|
C7 |
0.256 |
0.280 |
0.242 |
0.213 |
0.187 |
0.255 |
0.255 |
1.687 |
0.241 |
Los pesos relativos de cada uno de los criterios en el conjunto de decisión para la ponderación de los valores de preferencia difusa son:
Wp = {0.24; 0.13; 0.08; 0.04; 0.03; 0.24; 0.24}, donde: 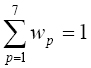
6. Relaciones difusas de preferencias en el conjunto de alternativas de la cartera de proyectos turísticos
La Relación Difusa de Preferencia (Rp), definida sobre un conjunto de alternativas X, expresa el grado de pertenencia (μ Rp) en que se cumple la afirmación “la alternativa x es no peor que la alternativa y”, donde (x,y) Є X. De este modo, dicha relación es un conjunto difuso sobre el producto cartesiano X x X, y a la vez una aplicación:
μ Rp: X x X → [0,1], Donde: μ Rp es la posibilidad de cumplirse “x es no peor que y”, μ Rp, toma valores en el intervalo [0,1]
La relación difusa de preferencia se define mediante una matriz, cuyas celdas contienen μRp(x,y), siendo “x” un elemento de la fila y “y” un elemento de la columna. Para nuestro caso del estudio de la prioridad en la selección de proyectos de una cartera de oportunidades, resulta obvio que la relación difusa de preferencia se expresa como el grado en que se cumple que: “x es no menos prioritario que y”.
Para definir las matrices de relaciones difusas de preferencias (Rp) en el conjunto de alternativas de proyectos turísticos objeto del estudio comparado, debemos realizarlo según cada criterio de evaluación Cj, j=1,…,7; Para ello, buscaremos la μRp que corresponde a cada elemento de la matriz según la pregunta ¿en qué grado de 0 al 1 el elemento “x” de la fila i es no menos prioritario que el elemento “y” de las columnas, desde la perspectiva del criterio en cuestión Cj?. La matriz de relación difusa de preferencia será reflexiva dado que ningún proyecto es “no menos prioritario” (no peor) que sí mismo, por lo que tendremos para cada criterio Cj, j=1,…,7, las matrices que expresan las relaciones difusas de preferencias Rpj.
Los expertos emitieron sus opiniones sobre cada uno de los criterios respecto a las tres alternativas y establecieron sus relaciones difusas de preferencias. Para generalizar estas opiniones, recogidas en siete matrices μ Rp(x,y) por cada experto, aplicamos el conjuntivo AND lógico del promedio geométrico.
En Rodríguez, Betancourt y Escobar (2006), se discuten las características de las t-normas más conocidas en la literatura para el uso como conjuntivo AND en la lógica difusa y se precisan sus limitaciones cuando se deben tomar en cuenta múltiples criterios de evaluación y donde la riqueza de información que aportan los expertos del sistema no debe ser desechada, y se propone el uso de la t-norma:
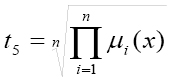
donde: μi (x) es la posibilidad de la influencia del criterio del experto i; n es la cantidad de expertos con criterios de valoración.
Esta expresión, que se denomina de media geométrica, cumple con las propiedades de una t-norma o sea; es no decreciente en cada argumento, conmutativa, asociativa y cumple con la condición de contorno definida para las t-normas. Como resultado se obtienen siete matrices de Relaciones Difusas de Preferencias, una por cada criterio de valoración:
|
C1 |
X1 |
X2 |
X3 |
C2 |
X1 |
X2 |
X3 |
C3 |
X1 |
X2 |
X3 |
C4 |
X1 |
X2 |
X3 |
|||
|
X1 |
1 |
0.5 |
0.3 |
X1 |
1 |
0.9 |
0.1 |
X1 |
1 |
0.4 |
0.1 |
X1 |
1 |
0.6 |
0.5 |
|||
|
X2 |
0.6 |
1 |
0.5 |
X2 |
0.2 |
1 |
0.3 |
X2 |
0.8 |
1 |
0.5 |
X2 |
0.5 |
1 |
0.3 |
|||
|
X3 |
0.6 |
0.5 |
1 |
X3 |
0.1 |
0.8 |
1 |
X3 |
0.7 |
0.4 |
1 |
X3 |
0.5 |
0.6 |
1 |
|
C5 |
X1 |
X2 |
X3 |
C6 |
X1 |
X2 |
X3 |
C7 |
X1 |
X2 |
X3 |
||
|
X1 |
1 |
0.9 |
0.2 |
X1 |
1 |
1 |
0.8 |
X1 |
1 |
1 |
0.8 |
||
|
X2 |
0.1 |
1 |
0.1 |
X2 |
0 |
1 |
0 |
X2 |
0 |
1 |
0 |
||
|
X3 |
0.7 |
0.7 |
1 |
X3 |
1 |
1 |
1 |
X3 |
1 |
1 |
1 |
Las matrices expresan el grado de cumplimiento de las relaciones difusas de preferencias Rp para los criterios Cj, j= 1,…,7. Teniendo en cuenta que cada criterio tiene un peso relativo diferente dentro del conjunto de valoración múltiple, la combinación convexa del conjunto difuso X1, X2, y X3 en X, se obtendrán por:
μwj (x,y)= wj* μj(x,y),
de lo que resulta;
|
C1w1 |
X1 |
X2 |
X3 |
C2w2 |
X1 |
X2 |
X3 |
C3w3 |
X1 |
X2 |
X3 |
C4w4 |
X1 |
X2 |
X3 |
|||
|
X1 |
0.24 |
0.12 |
0.07 |
X1 |
0.13 |
0.12 |
0.01 |
X1 |
0.08 |
0.03 |
0.01 |
X1 |
0.04 |
0.02 |
0.02 |
|||
|
X2 |
0.15 |
0.24 |
0.12 |
X2 |
0.03 |
0.13 |
0.04 |
X2 |
0.06 |
0.08 |
0.04 |
X2 |
0.02 |
0.04 |
0.01 |
|||
|
X3 |
0.15 |
0.12 |
0.24 |
X3 |
0.01 |
0.10 |
0.13 |
X3 |
0.05 |
0.03 |
0.08 |
X3 |
0.02 |
0.02 |
0.04 |
|
C5w5 |
X1 |
X2 |
X3 |
C6w6 |
X1 |
X2 |
X3 |
C7w7 |
X1 |
X2 |
X3 |
||
|
X1 |
0.02 |
0.02 |
0.00 |
X1 |
0.24 |
0.24 |
0.19 |
X1 |
0.24 |
0.24 |
0.19 |
||
|
X2 |
0.00 |
0.02 |
0.00 |
X2 |
0.00 |
0.24 |
0.00 |
X2 |
0.00 |
0.24 |
0.00 |
||
|
X3 |
0.02 |
0.02 |
0.02 |
X3 |
0.24 |
0.24 |
0.24 |
X3 |
0.24 |
0.24 |
0.24 |
7. Selección de la alternativa óptima, con la ayuda de la relación difusa de preferencia rigurosa.
Dado el hecho de que existen siete criterios de comparación expresados por las relaciones difusas de preferencias con pesos relativos diferentes de las tres alternativas, se requiere sintetizarlas en una sola matriz que globalice la información, denominada matriz de preferencia, Q2, determinada a partir de la suma de las celdas semejantes de las relaciones de preferencias por cada criterio, mediante:
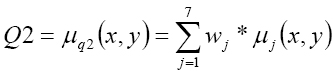
La relación de preferencia rigurosa Q2r, μRq2 correspondiente a Q2 se logra aplicando el algoritmo:

Estas dan paso a la determinación del subconjunto de alternativas no dominadas al máximo, correspondiente a Q2:
1 - μmax= {1-μ1max, 1-μ2max, 1-μ3max}
Como resultado se obtienen las valoraciones definitivas de cada una de las alternativas. Al ejecutarse el procedimiento apuntado arriba, se obtiene el siguiente resultado que se detalla por sus pasos:
1.Construir la relación de preferencia Q2, sobre la base de la suma ponderada según el coeficiente wi calculado para cada alternativa y criterio, de las celdas similares, resulta la matriz:
|
Q2 |
X1 |
X2 |
X3 |
|
X1 |
1.00 |
0.80 |
0.51 |
|
X2 |
0.26 |
1.00 |
0.21 |
|
X3 |
0.73 |
0.78 |
1.00 |
2.Determinar la relación de preferencia rigurosa Q2r, μRq2 correspondiente a Q2 aplicando el algoritmo, ΜRq1:
De lo que obtenemos a Q2r como:
|
Q2r |
X1 |
X2 |
X3 |
|
X1 |
0.00 |
0.54 |
0.00 |
|
X2 |
0.00 |
0.00 |
0.00 |
|
X3 |
0.23 |
0.57 |
0.00 |
3.Determinar el subconjunto de alternativas no dominadas al máximo en Q2,
μmax= {0.23; 0.57; 0} y
1- μmax= {0.77; 0.43; 1}
Por lo que tendremos:
|
Hotel Tararaco, Ampliación y mejora |
Hotel Residencial Santa Lucía |
Base Náutica La Boca con 100 Atraques |
|
0.77 |
0.509 |
1 |
De lo que resulta, que el proyecto de Nuevo Producto Náutico en el destino Playa Santa Lucia es el más prioritario, no dominado al máximo, respecto a los otros dos miembros del conjunto difuso de alternativas de Proyectos X, definidos en este estudio comparado, la renovación radical de producto hotelero (ampliación y mejora) tiene a juicio de los expertos una segunda prioridad.
Este resultado cuantitativo, permite encontrar respuestas que solo de forma cualitativa no nos era posible dar, atendiendo a los múltiples atributos de la decisión, la vaguedad de los datos y dada la aparente incomparabilidad de la naturaleza de los proyectos. Es de resaltar que el valor absoluto de pertenencia o grado de membresía solo especifica un orden de las comparaciones en una escala ordinal y su valor continuo en una escala métrica pierde todo significado fuera del orden de comparación de estas tres alternativas.
8. Conclusiones
El procedimiento de la identificación de indicadores y las herramientas para la toma de decisiones, mediante la ordenación comparada de mejor a peor de los proyectos turísticos en Camagüey, en una aplicación de las relaciones de preferencia borrosas, es pertinente y adecuado a la selección de proyectos turísticos atendiendo a las necesidades de jerarquizar los proyectos que impacten en el desarrollo dentro de las restricciones de recursos. Se cumple el objetivo de una propuesta adecuada a las condiciones de incertidumbre, ofreciendo un enfoque integral de la selección no reducida a indicadores económicos financieros.
En un ejercicio de validación sobre tres proyectos de disímiles naturaleza e impacto sobre el turismo en el destino Playa Santa Lucía, los expertos a través del procedimiento y sus herramientas, sugieren priorizar el proyecto de nuevo producto náutico sobre los proyectos hoteleros y dentro de los hoteleros, la renovación radical frente a nueva instalación.
REFERENCIAS BIBLIOGRÁFICAS
y (2017). La evaluación financiera de proyectos y su aporte en la generación de valor corporativo. Ciencia y Poder Aéreo. Revista Científica de la Escuela de Postgrados de la Fuerza Aérea Colombiana, (12), 144-155, DOI: http://dx.doi.org/10.18667/cienciaypoderaereo.567
y (2021). Análisis de decisiones multicriterio en la integración de herramientas de la economía ecológica. Revista Universidad y Sociedad, 13(4), 468-477. Recuperado de https://rus.ucf.edu.cu
(2013). La aplicación del juicio de experto como técnica de evaluación de las tecnologías de la información y comunicación (TIC). Revista de Tecnología de Información y Comunicación en Educación 2013, 7 (2). Recuperado de https://dialnet.unirioja.es/servlet/articulo?codigo=4857163.
Cubadebate. (2022). Cuba recibe en 2021 más de medio millón de visitantes extranjeros. Recuperado de http://www.cubadebate.cu/noticias/2022/02/06/cuba-recibe-en-2021-mas-de-medio-millon-de-visitantes-extranjeros/
(2001). Gestión de Competencias. La Habana: Editorial Academia.
y (2017). Fuzzy analytic hierarchy process. Boca Raton: CRC Press, 2017.
, y (2018). Aplicación de la lógica difusa en proyectos. EPISTEMUS, 7-14. Recuperado de https://dspace.uclv.edu.cu
y (2008). Evaluación y clasificación de las técnicas utilizadas por las organizaciones, en las últimas décadas, para seleccionar proyectos. Revista de Métodos Cuantitativos para la Economía y la Empresa, (5), 67–115. Recuperado de http://www.upo.es/RevMetCuant/art20.pdf
y (2007). Evaluación y clasificación en grupos empleando relaciones de preferencia borrosas. Revista Eletrônica Sistemas & Gestão, 2(1), 16-35. Recuperado de https://www.revistasg.uff.br/sg/article/view/SGV2NA2
y (1996). Fuzzy multicriteria decision making: Recent developments. Fuzzy Sets and Systems. 78, 139-153.
(2021). Análisis y selección de vehículos mediante aplicación de métodos multi-criterio: AHP y ELECTRE. (Tesis de maestría, Universidad de Sevilla, España). Recuperado de https://biblus.us.es
(1995). Dirección Integrada de proyectos - DIP - Project Management. 2da Edición. Madrid: Universidad Politécnica de Madrid.
ISO 10006:2017. Quality management — Guidelines for quality management in projects. Recuperado de https://www.iso.org/standard/70376.html
y (2020). La lógica borrosa y su importancia en la búsqueda y recuperación de información en la web. Universidad y Sociedad, 12(2), 306-311. Recuperado de https://rus.ucf.edu.cu
, y (2018). Modelo para la jerarquización y selección de proyectos de iniciativas municipales de desarrollo local. Retos de la Dirección 2018; 12(1). Recuperado de http://scielo.sld.cu/
y (2018). Proyecto comunitario (Turístico-Cultural): Boulevard Maroya. (Validación). Revista electrónica Ciencia Digital, 2(3), 173-186. Recuperado de http://cienciadigital.org
MEP (2014). Reglamento del proceso inversionista. Decreto No. 327 del Consejo de Ministros. Gaceta Oficial No. 5 Extraordinaria de 23 de enero 2015.
Mesa Redonda. (9 de septiembre de 2021). Cómo se prepara el turismo para la reapertura de fronteras. [Archivo de vídeo]. Recuperado de https://m.youtube.com/watch?v=oN-VuyTB3fk&feature=youtu.be
(2019). El método Analytic Hierarchy Process para la toma de decisiones. Repaso de la metodología y aplicaciones. Investigación Operativa, 27(46), 54-73. Recuperado de https://revistas.unc.edu.ar
y (2015). Estudio comparativo aplicado entre una técnica de toma de decisiones multicriterio difusa y la metodología Press II multiexperto. www.uv.es
Oficina Nacional de Estadística e Información. (2021). Anuario Estadístico de Cuba 2020. Capítulo 15: Turismo (Edición 2021). Recuperado de http://www.onei.gob.cu/sites/default/files/15_turismo.pdf
(1981). Problemas de la toma de decisiones en condiciones de la información inicial difusa. Moscú, Nauka.
, y (2019). Evaluación técnica y financiera de proyectos productivos aplicando lógica difusa. CIENCIAMATRIA. Revista Interdisciplinaria de Humanidades, Educación, Ciencia y Tecnología, 5(1), 298-327. DOI 10.35381/cm.v5i1.268
Ostelea. (2021). Tendencias en turismo para el 2022. Recuperado de https://www.ostelea.com/actualidad/blog-turismo/tendencias-en-turismo/tendencias-en-turismo
PMBOK (2017). Guía de los fundamentos para la dirección de proyectos. Sexta Edición. Pennsylvania: Project Management Institute.
(2018). Propuesta de un método de selección de proyectos de infraestructura universitaria, mediante un análisis multicriterio. (Tesis de pregrado, Universidad del Valle, Palmira, Colombia). Recuperado de https://www.bibliotecadigital.univalle.edu.co
y (2019). El proceso de selección de proyectos en las incubadoras de empresas. Propuesta de procedimiento para una incubadora universitaria cubana. Revista Internacional de Gestión del Conocimiento y la Tecnología 2019; 7(2). Recuperado de https://www.researchgate.net
(2018). Lógica Difusa para la toma de decisiones. Desarrollo de un aplicativo móvil para la aprobación de propuestas de proyectos. (Tesis de pregrado, Universidad Católica de Santiago de Guayaquil, Ecuador). Recuperado de https://repositorio.ucsg.edu.ec/handle/3317/11377
, , (2022). Turismo de naturaleza en la modalidad de agroturismo para el desarrollo local sostenible en Guamuhaya. Revista Universidad y Sociedad, 14(5), 204-214. Epub 30 de octubre de 2022. Recuperado en 19 de octubre de 2024, de http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S2218-36202022000500204&lng=es&tlng=es.
(2006). El Estudio comparado de la competitividad turística, una aplicación de la lógica difusa de preferencia. Revista Retos Turísticos, No 1 y 2 (2006). Universidad de Matanzas.
(Ed.). (2012). Estudio del ciclo de vida de los destinos de sol y playa: Playas del Este, Jibacoa, Cayo Largo, Varadero, Ancón, Jardines del Rey, Playa Santa Lucía, Marea del Portillo y Holguín. Propuestas para su dinamización. Resumen ejecutivo del proyecto.
y (2020). Números neutrosóficos de valor único y proceso analítico jerárquico para la discriminación de proyectos. Revista Investigación Operacional, 41(5), 751-760. Recuperado de https://rev-inv-ope.pantheonsorbonne.fr/sites/default/files/inline-files/41520-17.pdf
y (2001). Models, methods, concepts & applications of the analytic hierarchy process. New York: Springer Science+Business Media
y (2019). El Turismo en Cuba: Desarrollo, Retos y Perspectivas. Rosa dos Ventos, 11(1), 23-49, DOI: https://doi.org/10.18226/21789061.v11i1p23
(2009). ATSocial, Proyecto: como parte de la organización Social. Recuperado de http://atsocial.blogspot.com
(2012). Modelo de selección de proyectos aplicando cuadro de mando integral y Scoring para empresas consultoras de tecnología de información. (Tesis de maestría, Universidad Nacional de Ingeniería, Lima, Perú). Recuperado de https://scholar.archive.org